景真

外观

二叉树最大宽度

约 980 字大约 3 分钟

DFSBFS

2025-02-28

662. 二叉树最大宽度

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

每一层的 宽度 被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位 带符号整数范围内。

示例 1：

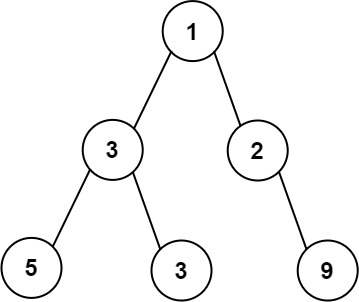
img.png

输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

提示：

  • 树中节点的数目范围是 [1, 3000]
  • -100 <= Node.val <= 100

层序遍历

class Solution {
    public int widthOfBinaryTree(TreeNode root) {
        if (root == null) {
            return 0;
        }
        
        int res = 1; // 初始化最大宽度为1
        Queue<Pair<TreeNode, Integer>> queue = new LinkedList<>(); // 用于存储当前层的节点及其索引。注意Pair类。
        queue.offer(new Pair<>(root, 1)); // 根节点的索引为1。注意初始化Pair实例的方法。

        // 使用广度优先搜索（BFS）遍历二叉树
        while (!queue.isEmpty()) {
            int size = queue.size();
            int start = queue.peek().getValue(); // 当前层的起始索引
            int end = queue.peek().getValue(); // 当前层的结束索引，初始化为起始索引

            for (int i = 0; i < size; i++) {
                Pair<TreeNode, Integer> pair = queue.poll();
                TreeNode node = pair.getKey();
                int index = pair.getValue();
                // 更新当前层的结束索引
                end = index;

                // 将子节点及其索引加入队列
                if (node.left != null) {
                    queue.offer(new Pair<>(node.left, index * 2));
                }
                if (node.right != null) {
                    queue.offer(new Pair<>(node.right, index * 2 + 1));
                }
            }

            // 计算当前层的宽度，并更新最大宽度
            res = Math.max(res, end - start + 1);
        }

        return res; // 返回最大宽度
    }
}
  • 时间复杂度： O(n)O(n)，其中 nn 是二叉树的节点个数。需要遍历所有节点。
  • 空间复杂度: O(n)O(n)。广度优先搜索的空间复杂度最多为 O(n)O(n) 。

有返回值有信息参数的DFS

使用哈希表记录每一层最左边节点的索引，计算本层、左右子树的最远距离，返回最大值。

class Solution {
    // 使用哈希表记录每一层最左边节点的索引
    Map<Integer, Integer> levelMin = new HashMap<>();

    public int widthOfBinaryTree(TreeNode root) {
        // 调用深度优先搜索方法。注意index是1，这样左子节点的索引才是index*2。深度无所谓。
        return dfs(root, 1, 1);
    }

    public int dfs(TreeNode node, int depth, int index) {
        // 如果节点为空，返回0
        if (node == null) {
            return 0;
        }

        // 将当前层的最左节点索引记录下来（如果未记录），注意putIfAbsent
        levelMin.putIfAbsent(depth, index);
        // 计算当前层的最远距离：当前节点索引 - 当前层最左节点的索引 + 1
        int currentWidth = index - levelMin.get(depth) + 1;

        // 递归计算左右子树的最远距离。索引是无条件增加的，即空节点也有索引。
        int leftWidth = dfs(node.left, depth + 1, index * 2);
        int rightWidth = dfs(node.right, depth + 1, index * 2 + 1);

        // 返回最远距离。左右子树的深度可能不一样，进而右子树的最远距离也未必大于左子树的最远距离，
        // 所以需要取左右子树的最远距离的最大值。当前节点也可能没有左右子树，所以最大值有可能是当前节点的最远距离。
        return Math.max(currentWidth, Math.max(leftWidth, rightWidth));
    }
}
  • 时间复杂度： O(n)O(n) ，其中 nn 是二叉树的节点个数。需要遍历所有节点。
  • 空间复杂度: O(n)O(n) 。递归的深度最多为 O(n)O(n) 。