450. 删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

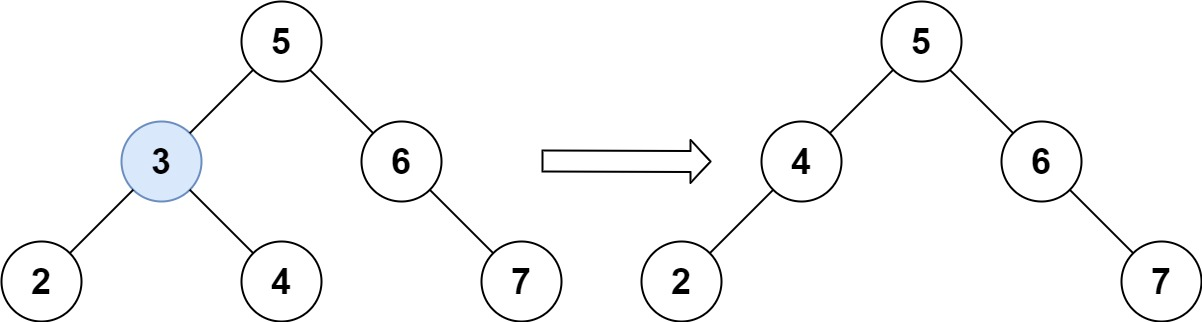
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

• 节点数的范围 [0, 104].
• -105 <= Node.val <= 105
• 节点值唯一
• root 是合法的二叉搜索树
• -105 <= key <= 105

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

有返回值有信息参数的DFS

对每个节点，先检查，再根据检查结果进入相应的子树进行操作。

先遍历，再操作。遍历二叉树，检查当前节点是否是要删除的节点

操作前要检查要删除的节点是否是叶子节点。

如果树为空，直接返回 null。如果当前节点的值大于要删除的值，递归删除左子树中的节点。 删除时要考虑删除的节点是否是叶子结点，如果不是，则需要找到右子树的最小节点，用它来补上空位。类似669. 修剪二叉搜索树。

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) {
            return null; // 如果树为空，直接返回 null
        }

        if (key < root.val) {
            // 如果要删除的节点值小于当前节点值，递归删除左子树中的节点
            root.left = deleteNode(root.left, key);
        } else if (key > root.val) {
            // 如果要删除的节点值大于当前节点值，递归删除右子树中的节点
            root.right = deleteNode(root.right, key);
        } else {
            // 找到要删除的节点
            if (root.left == null) {
                // 如果要删除的节点没有左子节点，返回右子节点作为新的根节点。重点。
                return root.right;
            } else if (root.right == null) {
                // 如果要删除的节点没有右子节点，返回左子节点作为新的根节点。重点。
                return root.left;
            }

            // 如果要删除的节点有两个子节点，找到右子树的最小节点（后继节点）
            TreeNode successor = findMin(root.right);
            // 将后继节点的值赋给当前节点
            root.val = successor.val;
            // 删除右子树中的后继节点，删除就是把该节点的父关系取消。重点。
            root.right = deleteNode(root.right, successor.val);
        }

        // 返回当前节点作为根节点
        return root;
    }

    private TreeNode findMin(TreeNode node) {
        // 最小节点位于最左边
        while (node.left != null) {
            node = node.left;
        }
        return node;
    }
}

• 时间复杂度：O(n)，其中 n 为 root 的节点个数。最差情况下，寻找和删除 successor 各需要遍历一次树。
• 空间复杂度：O(h)，其中 h 为树的高度。最大为 O(n)。