226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

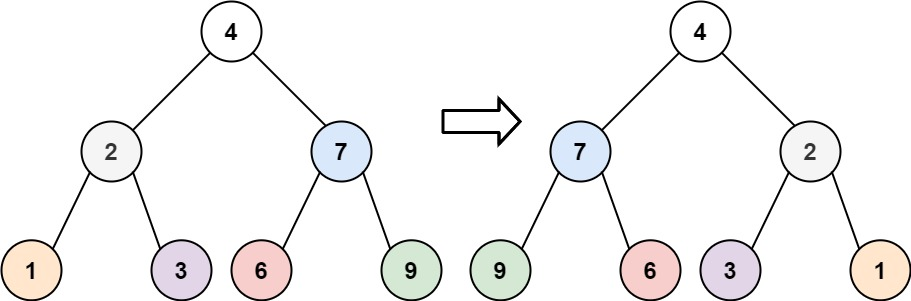
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

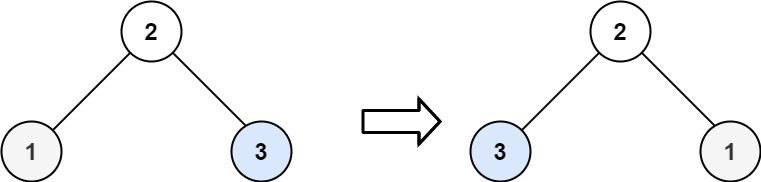
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目范围在 [0, 100] 内
• -100 <= Node.val <= 100

递归-后序遍历-归并，有返回值

先翻转左右子树，保存起来，然后交换左右子节点，最后返回根节点。先操作左右子树，再合并。

后序遍历有返回值，类似动态规划。前序遍历没有，类似回溯。

class Solution {
    // 定义：将以 root 为根的这棵二叉树翻转，返回翻转后的二叉树的根节点。后序一定要注意返回值。
    TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        
        // 利用函数定义，先翻转左右子树，保存起来
        TreeNode left = invertTree(root.left);
        TreeNode right = invertTree(root.right);

        // 然后交换左右子节点
        root.left = right;
        root.right = left;

        // 和定义逻辑自洽：以 root 为根的这棵二叉树已经被翻转，返回 root
        return root;
    }
}

• 时间复杂度：O(N)，其中 N 为二叉树节点的数目。我们会遍历二叉树中的每一个节点，对每个节点而言，我们在常数时间内交换其两棵子树。
• 空间复杂度：O(N)。使用的空间由递归栈的深度决定，它等于当前节点在二叉树中的高度。在平均情况下，二叉树的高度与节点个数为对数关系，即 O(log⁡N)。而在最坏情况下，树形成链状，空间复杂度为 O(N)。

递归-前序遍历，无返回值

先交换根节点的左右子节点，再去递归操作左右子树。先操作，再递归。

先操作当前节点，再操作左右子节点。

class Solution {
    public TreeNode invertTree(TreeNode root) {
        traverse(root);
        return root;
    }

    void traverse(TreeNode root) {
        if (root == null) {
            return;
        }
        
        // 每一个节点需要做的事就是交换它的左右子节点
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;

        // 遍历框架，去遍历左右子树的节点
        traverse(root.left);
        traverse(root.right);
    }
}

• 时间复杂度：O(N)，其中 N 为二叉树节点的数目。我们会遍历二叉树中的每一个节点，对每个节点而言，我们在常数时间内交换其两棵子树。
• 空间复杂度：O(N)。使用的空间由递归栈的深度决定，它等于当前节点在二叉树中的高度。在平均情况下，二叉树的高度与节点个数为对数关系，即 O(log⁡N)。而在最坏情况下，树形成链状，空间复杂度为 O(N)。