48. 旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在** 原地** 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

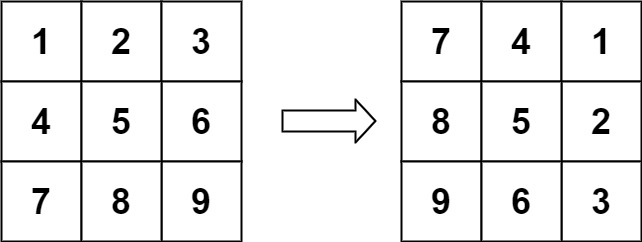
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

先转置再反转每一行

先把二维矩阵沿对角线反转，然后反转矩阵的每一行，结果就是顺时针反转整个矩阵。

matrix[i][j] → matrix[j][n-1-i]

通过上面的两个步骤操作：

1. 沿主对角线反转：
   • matrix[i][j] → matrix[j][i]
2. 反转每一行：
   • matrix[j][i] → matrix[j][n-1-i]

旋转等于反射的乘积，先沿对角线反射，再沿y轴反射

Erlangen program

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        
        // 先沿主对角线反转二维矩阵。先交换第一行和第一列，再交换第二行和第二列……
        // i=0时，matrix[0][j]是第一行，matrix[j][0]是第一列
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                // swap(matrix[i][j], matrix[j][i]);
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
        
        // 然后反转二维矩阵的每一行
        for (int[] row : matrix) {
            reverse(row);
        }
    }

    // 相向指针反转一维数组
    void reverse(int[] arr) {
        int i = 0, j = arr.length - 1;
        
        while (j > i) {
            // swap(arr[i], arr[j]);
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
            
            i++;
            j--;
        }
    }
}

时间复杂度O(n^2)，空间复杂度O(1)。

因此，内层循环总共执行的次数是：(n-1) + (n-2) + ... + 1，这与高斯求和公式相同，等于 n(n-1)/2。

反转每一行的时间复杂度为 O(n * n/2) = O(n^2)。