106. 从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

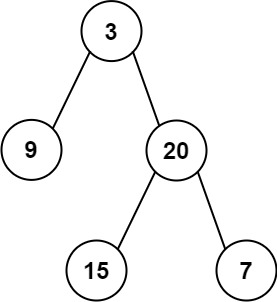
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

有返回值有信心参数的DFS，哈希表ValToIndex

构造二叉树，第一件事一定是找根节点，然后想办法构造左右子树。

后序遍历结果最后一个就是根节点的值，然后再根据中序遍历结果确定左右子树的节点。

class Solution {
    // 存储 inorder 中值到索引的映射
    Map<Integer, Integer> valToIndex = new HashMap<>();

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        for (int i = 0; i < inorder.length; i++) {
            valToIndex.put(inorder[i], i);
        }
        return build(inorder, 0, inorder.length - 1,
                    postorder, 0, postorder.length - 1);
    }

    /*
       定义：
       中序遍历数组为 inorder[inStart..inEnd]，
       后序遍历数组为 postorder[postStart..postEnd]，
       构造这个二叉树并返回该二叉树的根节点
    */
    TreeNode build(int[] inorder, int inStart, int inEnd,
                int[] postorder, int postStart, int postEnd) {
        if (inStart > inEnd) {
            return null;
        }
        
        // root 节点对应的值就是后序遍历数组的最后一个元素
        int rootVal = postorder[postEnd];
        TreeNode root = new TreeNode(rootVal);
        
        // rootVal 在中序遍历数组中的索引。重点。
        int index = valToIndex.get(rootVal);
        // 左子树的节点个数
        int leftSize = index - inStart;
        // 递归构造左右子树
        root.left = build(inorder, inStart, index - 1,
                         postorder, postStart, postStart + leftSize - 1);
        root.right = build(inorder, index + 1, inEnd,
                          postorder, postStart + leftSize, postEnd - 1);
                          
        return root;
    }
}

• 时间复杂度：O(n)，其中 n 是树中的节点个数。
• 空间复杂度：O(n)。我们需要使用 O(n) 的空间存储哈希表，以及 O(h)（其中 h 是树的高度）的空间表示递归时栈空间。这里 h<n，所以总空间复杂度为 O(n)。