654. 最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

1. 创建一个根节点，其值为 nums 中的最大值。
2. 递归地在最大值 左边 的 子数组前缀上 构建左子树。
3. 递归地在最大值 右边 的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

示例 1：

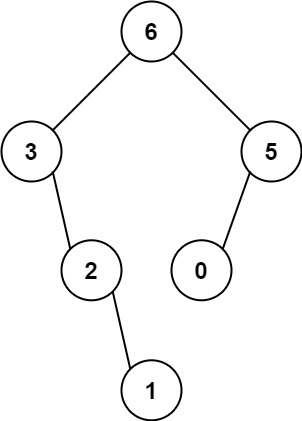
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000
• nums 中的所有整数 互不相同

递归

类似106. 从中序与后序遍历序列构造二叉树

import java.util.Scanner;

// 定义二叉树的节点
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x) {
        val = x;
    }
}

class Solution {
    // 主函数
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return build(nums, 0, nums.length - 1);
    }

    // 定义：将 nums[lo..hi] 构造成符合条件的树，返回根节点
    TreeNode build(int[] nums, int lo, int hi) {
        // 结束条件
        if (lo > hi) {
            return null;
        }

        // 找到数组中的最大值和对应的索引
        int index = -1, maxVal = Integer.MIN_VALUE;
        for (int i = lo; i <= hi; i++) {
            if (maxVal < nums[i]) {
                index = i;
                maxVal = nums[i];
            }
        }

        TreeNode root = new TreeNode(maxVal);
        // 递归调用构造左右子树
        root.left = build(nums, lo, index - 1);
        root.right = build(nums, index + 1, hi);

        return root;
    }

    // 进行前序遍历并打印树的结构
    public void printPreOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        System.out.print(root.val + " ");
        printPreOrder(root.left);
        printPreOrder(root.right);
    }

    // 进行中序遍历并打印树的结构
    public void printInOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        printInOrder(root.left);
        System.out.print(root.val + " ");
        printInOrder(root.right);
    }

    // 进行后序遍历并打印树的结构
    public void printPostOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        printPostOrder(root.left);
        printPostOrder(root.right);
        System.out.print(root.val + " ");
    }
}

// 主类，处理输入输出并调用构造二叉树的方法
public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        // 输入数组长度
        System.out.println("请输入数组的长度：");
        int n = scanner.nextInt();

        // 输入数组元素
        int[] nums = new int[n];
        System.out.println("请输入数组元素：");
        for (int i = 0; i < n; i++) {
            nums[i] = scanner.nextInt();
        }

        // 创建 Solution 对象并构造二叉树
        Solution solution = new Solution();
        TreeNode root = solution.constructMaximumBinaryTree(nums);

        // 打印树的前序遍历
        System.out.println("前序遍历结果：");
        solution.printPreOrder(root);
        System.out.println();

        // 打印树的中序遍历
        System.out.println("中序遍历结果：");
        solution.printInOrder(root);
        System.out.println();

        // 打印树的后序遍历
        System.out.println("后序遍历结果：");
        solution.printPostOrder(root);
        System.out.println();

        scanner.close();
    }
}

• 时间复杂度：O(n^2)，其中 n 是数组 nums 的长度。在最坏的情况下，数组严格递增或递减，需要递归 n 层，第 i (0≤i<n) 层需要遍历 n-i 个元素以找出最大值，总时间复杂度为 O(n^2)。
• 空间复杂度：O(n)，即为最坏情况下需要使用的栈空间。