98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

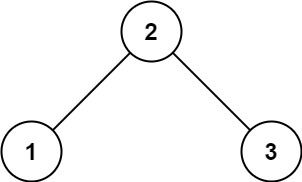
输入：root = [2,1,3]
输出：true

示例 2：

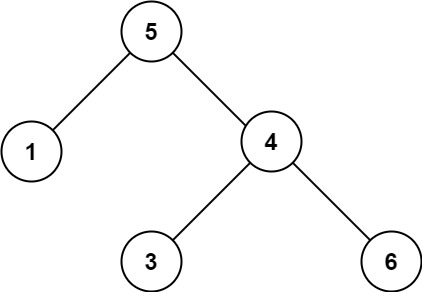
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -2^31 <= Node.val <= 2^31 - 1

前序遍历，归并结果

左子树的上界是根节点的值，下界是最小值。右子树的上界是最大值，下界是根节点的值。

public class Solution {
    // 主函数，检查树是否为有效的二叉搜索树
    public boolean isValidBST(TreeNode root) {
        // 调用辅助函数，初始范围设为 [Long.MIN_VALUE, Long.MAX_VALUE]
        // 因为节点值可能取到Integer的最小值或最大值，因此范围应该是Long的最小值和最大值。
        return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    // 辅助函数，递归检查树是否为有效的二叉搜索树
    public boolean isValidBST(TreeNode node, long lower, long upper) {
        // 递归结束条件。如果当前节点为空，返回 true（空树是有效的二叉搜索树）
        if (node == null) {
            return true;
        }
        // 特殊条件。如果当前节点的值不在合法范围内，返回 false
        if (node.val <= lower || node.val >= upper) {
            return false;
        }
        
        // 递归检查左子树和右子树
        // 对左子树，当前节点值是新的上界
        // 对右子树，当前节点值是新的下界
        return isValidBST(node.left, lower, node.val) && isValidBST(node.right, node.val, upper);
    }
}

• 时间复杂度: $O(n)$，其中 $n$ 为二叉树的节点个数。在递归调用的时候二叉树的每个节点最多被访问一次，因此时间复杂度为 $O(n)$。
• 空间复杂度: $O(n)$，其中 $n$ 为二叉树的节点个数。递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，即二叉树的高度。最坏情况下二叉树为一条链，树的高度为 $n$ ，递归最深达到 $n$ 层，故最坏情况下空间复杂度为 $O(n)$。

中序遍历

根据递归写迭代形式的解法。

结束条件，节点为空，返回true。

先递归遍历左子树，再检查当前节点值是否大于前一个中序遍历的节点值，并更新更新中序遍历的前一个节点值为当前节点值。最后递归遍历右子树。

class Solution {
    // 为什么要用-Long.MAX_VALUE？因为一开始比较的时候 node.val 必须大于 -Integer.MAX_VALUE
    private long inorder = -Long.MAX_VALUE;

    public boolean isValidBST(TreeNode root) {
        return inorderTraversal(root);
    }

    private boolean inorderTraversal(TreeNode node) {
        if (node == null) {
            return true;
        }

        // 递归遍历左子树
        if (!inorderTraversal(node.left)) {
            return false;
        }
        // 检查当前节点值是否大于前一个中序遍历的节点值。此时inorder的值是左子树的最右下的节点的值。
        if (node.val <= inorder) {
            return false;
        }
        // 更新inorder为当前节点值，以方便下次递归时与中序遍历的下一个节点比较。重点。
        inorder = node.val;
        // 递归遍历右子树
        return inorderTraversal(node.right);
    }
}

根据递归可以写迭代形式的中序遍历，即把栈描述出来。