在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。

例子：

[1,3,4,2,5]

1左边比1小的数，没有；

3左边比3小的数，1；

4左边比4小的数，1、3；

2左边比2小的数，1；

5左边比5小的数，1、3、4、2；

所以小和为1+1+3+1+1+3+4+2=16

要求时间复杂度O(NlogN)，空间复杂度O(N)

归并

最容易想到的做法是遍历一遍数组，对于每个元素计算前面比它小的数的和，累加即可得出结果，时间复杂度是O(N²)。

本题的更好的算法是借助 「归并排序」的思路。 smallSum([1,3,4,2,5])实际就等于smallSum([1,3,4])+smallSum([2,5])+c。之所以还有个c， 是因为左半段数组中可能存在比右半段数组小的元素，这个不能遗漏。通过归并排序的merge过程，我们可以很方便计算这个c。

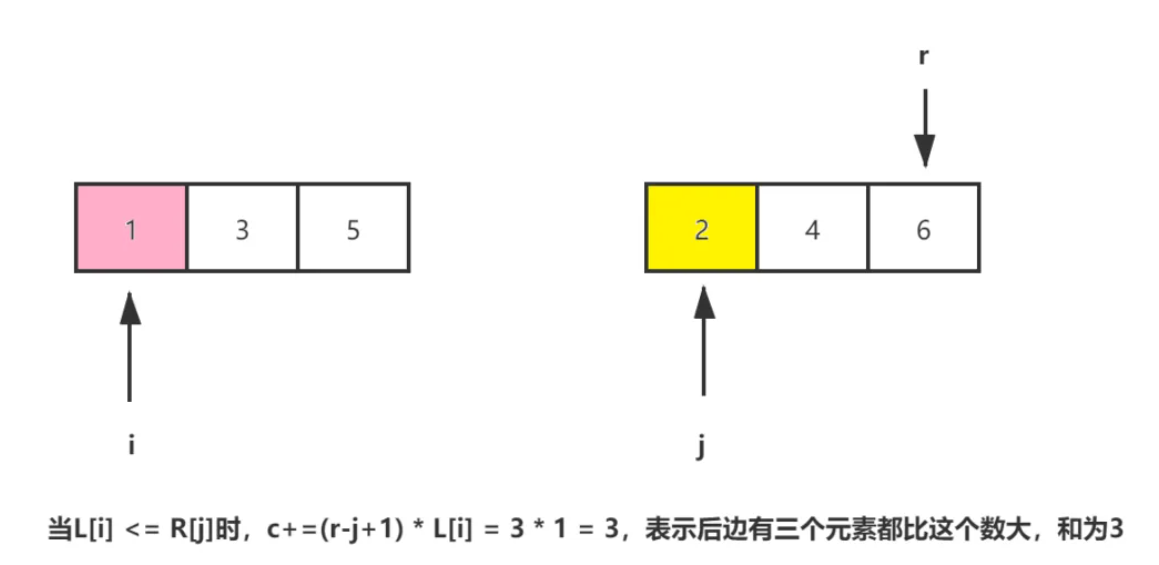
在merge时，左段数组L和右段数组R都是有序的了。结合下边的示意图，当L[i]<=R[j]时，表示L[i]比R[j]~R[r]的元素都要小。 因此c需加上j及以后元素的个数*L[i]，即c+=(r-j+1) * L[i]。

import java.util.Scanner;

public class Solution {
    // 定义数组大小常量
    private static final int N = 100010;
    // 定义两个数组：nums存储原始数据，temp用于归并时临时存储
    private static int[] nums = new int[N];
    // temp数组可复用
    private static int[] temp = new int[N];

    // 归并排序中的归并过程，同时计算小和。注意多了一个r参数，就是为了计算小和。
    public static long merge(int[] a, int l, int mid, int r) {
        int i = l, j = mid + 1, k = 0;
        // 注意是long
        long res = 0;

        // 归并排序时，顺带计算左侧比右侧小的值贡献的小和
        while (i <= mid && j <= r) {
            if (a[i] <= a[j]) {
                // [r...j]中每个元素都比a[i]大，所以a[i]对小和的贡献为(r-j+1)*a[i]
                res += (r - j + 1) * (long) a[i]; // 计算小和。a[i]小于j，所以j的贡献中包括a[i]，其它同理。
                temp[k++] = a[i++];
            } else {
                temp[k++] = a[j++];
            }
        }

        // 如果左半部分还没有合并完，继续合并
        while (i <= mid) temp[k++] = a[i++];
        // 如果右半部分还没有合并完，继续合并
        while (j <= r) temp[k++] = a[j++];

        // 将temp中的内容拷贝回原数组a中。重点。
        // 注意a的范围是[l, r]，temp的范围是[0, r-l]
        for (i = l, k = 0; i <= r; i++) {
            a[i] = temp[k++];
        }
        // 注意返回是的res不是数组！
        return res;
    }

    // 归并排序，并计算数组的小和
    public static long getSmallSum(int[] a, int l, int r) {
        if (l == r) return 0;
        int mid = (l + r) / 2;

        // 分治递归处理左半部分和右半部分
        long L = getSmallSum(a, l, mid);
        long R = getSmallSum(a, mid + 1, r);

        // 合并左右部分，并计算合并时产生的小和
        long c = merge(a, l, mid, r);
        return L + R + c;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        
        // 读取输入
        for (int i = 0; i < n; i++) {
            nums[i] = sc.nextInt();
        }
        
        // 计算小和并输出结果
        System.out.println(getSmallSum(nums, 0, n - 1));
        
        sc.close();
    }
}

ASCII图解：

输入数组：nums = [1, 3, 2, 4]

分治过程：
            [1, 3, 2, 4]
           /             \
       [1, 3]           [2, 4]
      /     \          /     \
    [1]     [3]      [2]     [4]

合并过程：
    合并 [1] 和 [3]:
    比较 1 < 3 -> 小和 += 1
    结果：[1, 3], 小和 = 1

    合并 [2] 和 [4]:
    比较 2 < 4 -> 小和 += 2
    结果：[2, 4], 小和 = 2

    合并 [1, 3] 和 [2, 4]:
    比较 1 < 2 -> 小和 += 2 (1 对 [2, 4] 的贡献)
    比较 3 < 4 -> 小和 += 3 (3 对 [4] 的贡献)
    结果：[1, 2, 3, 4], 小和 = 5

总小和：1 + 2 + 5 = 8