404. 左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

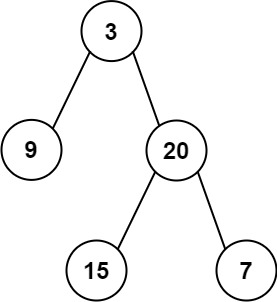
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:

输入: root = [1]
输出: 0

提示:

• 节点数在 [1, 1000] 范围内
• -1000 <= Node.val <= 1000

遍历二叉树时要注意两个条件，一个是平凡条件（一般是判空），一个是递归结束条件（一般是叶子节点，本题中是遇到左叶子节点才结束）。

无返回值无信息参数的DFS，全局变量

前序遍历，结束条件是递归到左叶子节点。采用全局变量，无返回值。

不需要回溯，因为我们只加不减。

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        dfs(root);
        return sum;
    }

    // 记录左叶子之和
    int sum = 0;
    // 二叉树遍历函数
    void dfs(TreeNode root) {
        if (root == null) {
            return;
        }

        // 前序位置，不能无条件累加当前节点的值，我们要算的是左叶子节点的和。
        // 注意这里操作的是当前节点和左子节点，不是只有当前节点。为什么要这样？
        // 因为左叶子节点=左+叶子，这一定需要两个节点才能判断。为什么不能通过当前节点和父节点判断？因为这样比较复杂。
        // 计入了当前节点的左叶子节点的值。
        if (root.left != null &&
            root.left.left == null && root.left.right == null) {
            // 找到左侧的叶子节点，记录累加值
            sum += root.left.val;
        }
        // 递归框架
        dfs(root.left);
        dfs(root.right);
    }
}

• 时间复杂度O(n)，n是二叉树的节点总数
• 空间复杂度O(h)，h是二叉树的高度

有返回值的DFS

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        // 调用递归函数，并从根节点开始。注意根节点不是左节点。
        return dfs(root, false);
    }

    private int dfs(TreeNode node, boolean isLeft) {
        if (node == null) {
            return 0; // 如果节点为空，返回 0
        }
        // 判断是否为左叶子节点。重点。
        if (node.left == null && node.right == null && isLeft) {
            return node.val; // 如果是左叶子节点，返回该节点的值
        }
        
        // 递归求取左子树和右子树的左叶子之和
        int leftSum = dfs(node.left, true);  // 左子树，标记为左节点
        int rightSum = dfs(node.right, false); // 右子树，标记为右节点
        
        // 返回左子树和右子树中所有左叶子节点的和
        return leftSum + rightSum;
    }
}

• 时间复杂度O(n)，n是二叉树的节点总数
• 空间复杂度O(h)，h是二叉树的高度