11. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

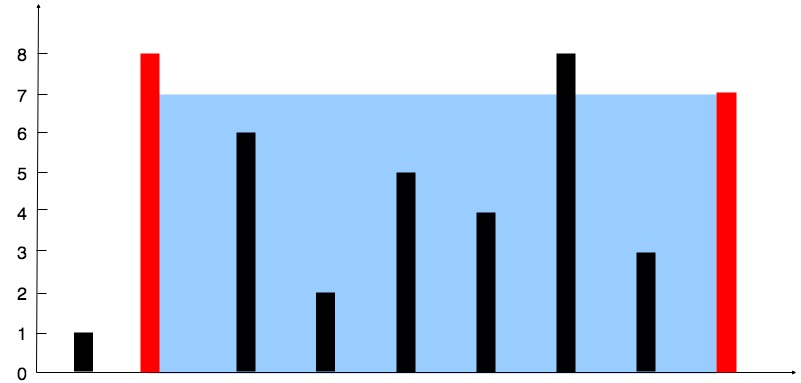
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

相向指针-求最大的矩形面积

注意本题中的元素是没有宽度的墙，即 [1,3] 的容器的宽度是2而不是1。

先计算面积，再移动指针。

接雨水问题给出的类似一幅直方图，每个横坐标都有宽度，而本题给出的每个横坐标是一条竖线，没有宽度。

为什么要移动较低的一边？

因为矩形的高度是由 min(height[left], height[right]) 即较低的一边决定的。你如果移动较低的那一边，那条边可能会变高，使得矩形的高度变大， 进而就「有可能」使得矩形的面积变大；相反，如果你去移动较高的那一边，矩形的高度是无论如何都不会变大的（就算高边变高了，矩形的高依然是取较低的那个高）， 所以不可能使矩形的面积变得更大。

class Solution {
    int maxArea(int[] height) {
        int left = 0, right = height.length - 1;
        int res = 0;
        
        while (left < right) {
            // [left, right] 之间的矩形面积，注意本题中的元素没有宽度的墙，即[1,3]的容器的宽度是2而不是1。
            int cur_area = Math.min(height[left], height[right]) * (right - left);
            // 每次计算完都要更新最大值
            res = Math.max(res, cur_area);
            
            // 双指针技巧，移动较低的一边
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
        
        return res;
    }
}

• 时间复杂度：$O(N)$，双指针总计最多遍历整个数组一次。
• 空间复杂度：$O(1)$，只需要额外的常数级别的空间。