581. 最短无序连续子数组

给你一个整数数组 nums ，你需要找出一个 连续子数组 ，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

请你找出符合题意的 最短 子数组，并输出它的长度。

示例 1：

输入：nums = [2,6,4,8,10,9,15]
输出：5
解释：你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。

示例 2：

输入：nums = [1,2,3,4]
输出：0

示例 3：

输入：nums = [1]
输出：0

提示：

• 1 <= nums.length <= 10^4
• -10^5 <= nums[i] <= 10^5

进阶：你可以设计一个时间复杂度为 O(n) 的解决方案吗？

双向约束问题。

副本排序

对副本进行排序，然后遍历，找到从左到右原数组和副本中第一个不同的元素索引 left，找到从右到左原数组和副本中第一个不同的元素索引。

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        // 创建数组的副本，并对副本进行排序
        int[] temp = Arrays.copyOf(nums, nums.length);
        Arrays.sort(temp);
        // 初始化左右边界
        int left = -1, right = -1;
        
        // 找到从左到右第一个不同的元素索引
        for (int i = 0; i < nums.length; i++) {
            if (temp[i] != nums[i]) {
                left = i;
                break;
            }
        }
        // 找到从右到左第一个不同的元素索引
        for (int i = nums.length - 1; i >= 0; i--) {
            if (temp[i] != nums[i]) {
                right = i;
                break;
            }
        }
        
        // 如果数组本来就是有序的，返回0。改成||也可以。事实上，left和right要么同时为原值，要么同时不为原值。
        // 因为涉及到交换，而交换是交换两个元素的位置，这两个位置一个就是左边界，一个是右边界。
        //if (left == Integer.MAX_VALUE && right == Integer.MIN_VALUE) {
        //    return 0;
        //}
        // 返回无序子数组的长度
        return left == right ? 0 : right - left + 1;
    }
}

• 时间复杂度: $O(n \log n)$ ，其中 $n$ 为给定数组的长度。我们需要 $O(n \log n)$ 的时间进行排序，以及 $O(n)$ 的时间遍历数组，因此总时间复杂度为 $O(n)$ 。
• 空间复杂度：$O(n)$，其中 $n$ 为给定数组的长度。我们需要额外的一个数组保存排序后的数组 numsSorted。

双向约束

从左到右遍历数组，找到右边界。右边界即小于已遍历元素的最大值的最后一个元素，即图中的F。从右到左遍历数组，找到左边界。 左边界即大于已遍历元素的最小值的最后一个元素，即图中的B。左右指针同时走，每次循环前进一步。

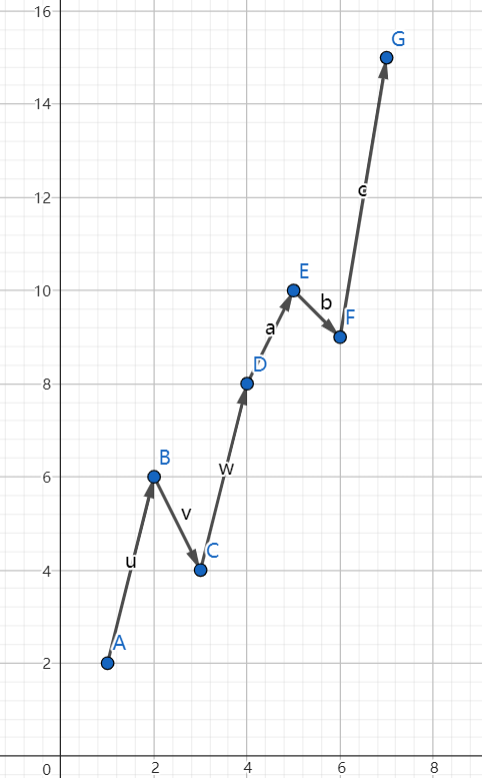
如果以最小值开始，以最大值结尾，那么左右边界在数组内部，反之在数组边界。

只要新元素比最大值大，就让新元素的位置是右边界。反之只更新最大值不更新右边界，因为目前出于升序段，没必要排序。

只要新元素比最小值小，就让新元素的位置是左边界。

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int n = nums.length;
        // 注意初始值。
        int max = Integer.MIN_VALUE, min = Integer.MAX_VALUE;
        // 注意初始值都是-1
        int start = -1, end = -1;

        // 从左到右找到第一个需要排序的最大值
        for (int i = 0; i < n; i++) {
            // 遇到小数，就更新右边界
            if (nums[i] < max) {
                end = i;
            } else { // 遇到大数，就更新最大值
                max = nums[i];
            }
        }

        // 从右到左找到第一个需要排序的最小值
        for (int i = n - 1; i >= 0; i--) {
            // 遇到大数，就更新左边界
            if (nums[i] > min) {
                start = i;
            } else { // 遇到小数，就更新最小值
                min = nums[i];
            }
        }

        // 计算需要排序的子数组长度
        return (end > start) ? (end - start + 1) : 0;
    }
}

• 时间复杂度：O(n)，其中 n 是给定数组的长度，我们仅需要遍历该数组一次。
• 空间复杂度：O(1)。我们只需要常数的空间保存若干变量。

为什么不能下面这么写？反例：12333，13222。原因是极大值未必一定位于末尾，极小值也是。 所以不能用极大极小值的位置。例如13222中，极小值是第一个2，但是我们应该用最后一个2的位置。

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int n = nums.length;
        int max = Integer.MIN_VALUE, min = Integer.MAX_VALUE;
        int start = -1, end = -1;

        // 从左到右找到第一个极大值
        for (int i = 0; i < n - 1; i++) {
            if (nums[i] >= nums[i+1]) {
                start = i;
                break;
            }
        }

        // 从右到左找到第一个极小值
        for (int i = n - 1; i > 0; i--) {
            if (nums[i] < nums[i-1]) {
                end = i;
                break;
            }
        }

        // 计算需要排序的子数组长度
        return (end > start) ? (end - start + 1) : 0;
    }
}