84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

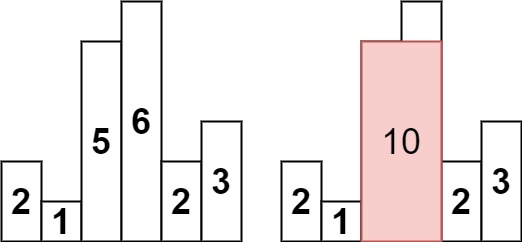
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

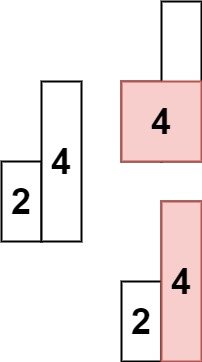
输入： heights = [2,4]
输出： 4

提示：

• 1 <= heights.length <=105
• 0 <= heights[i] <= 104

递增栈

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;  // 获取数组长度
        int[] left = new int[n];  // 存储每个柱子左边第一个小于它的柱子的索引
        int[] right = new int[n]; // 存储每个柱子右边第一个小于它的柱子的索引
        Arrays.fill(right, n);    // 初始化 right 数组，默认为 n。重点。
        Deque<Integer> mono_stack = new ArrayDeque<>(); // 单调栈，用于存储柱子的索引

        // 正序遍历每个柱子，计算它在 left 和 right 数组中的值。入栈前计算right数组，入栈后计算left数组。
        for (int i = 0; i < n; ++i) {
            // 维护单调栈，保证栈中柱子高度递增
            // 对同一个元素，入栈时计算left（left[当前元素]=栈顶元素），出栈时计算right（right[栈内元素]=当前元素）。
            // 对于当前元素，如果栈顶元素大于等于当前元素，就计算栈顶元素的right数组，然后弹出栈顶元素，直到栈顶元素小于当前元素。
            // 然后再计算当前元素的left数组，然后当前元素入栈。
            while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
                right[mono_stack.peek()] = i; // 更新 right 数组，当前元素小于栈顶元素
                mono_stack.pop(); // 栈顶元素出栈
            }
            left[i] = (mono_stack.isEmpty() ? -1 : mono_stack.peek()); // 更新 left 数组。注意-1！
            mono_stack.push(i); // 当前柱子入栈
        }

        int ans = 0; // 初始化最大矩形面积
        // 遍历每个柱子，计算以当前柱子高度为最小高度的矩形面积
        for (int i = 0; i < n; ++i) {
            int width = right[i] - left[i] - 1; // 计算矩形的宽度。重点。
            int area = width * heights[i]; // 计算矩形面积
            ans = Math.max(ans, area); // 更新最大矩形面积
        }
        return ans; // 返回最大矩形面积
    }
}

• 时间复杂度：O(N)
• 空间复杂度：O(N)