695. 岛屿的最大面积

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

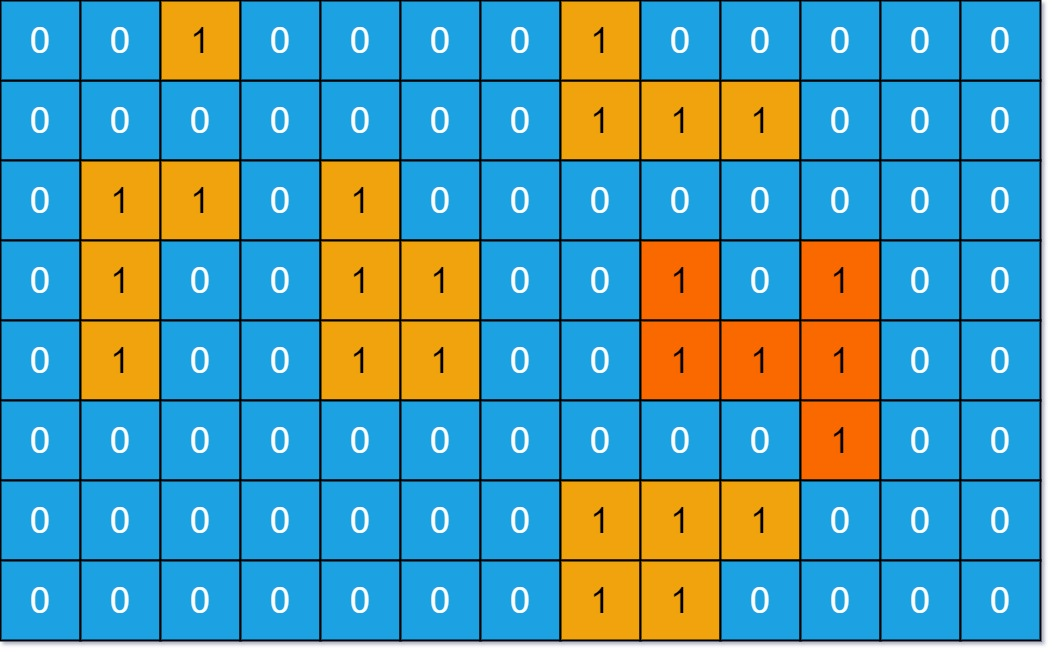
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• grid[i][j] 为 0 或 1

本题要注意不能用for循环遍历8个方向，应该是4个方向。

有返回值无信息参数的DFS，无条件前进。淹没是为了避免重复访问。

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        // 记录岛屿的最大面积
        int res = 0;
        int m = grid.length, n = grid[0].length;
        
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) {
                    // 淹没岛屿，并更新最大岛屿面积
                    res = Math.max(res, dfs(grid, i, j));
                }
            }
        }
        return res;
    }

    // 淹没与 (i, j) 相邻的陆地，并返回淹没的陆地面积。重点。
    int dfs(int[][] grid, int i, int j) {
        int m = grid.length, n = grid[0].length;
        if (i < 0 || j < 0 || i >= m || j >= n) {
            // 超出索引边界
            return 0;
        }
        if (grid[i][j] == 0) {
            // 已经是海水了
            return 0;
        }
        
        // 将 (i, j) 变成海水
        grid[i][j] = 0;
        return dfs(grid, i + 1, j)
                + dfs(grid, i, j + 1)
                + dfs(grid, i - 1, j)
                + dfs(grid, i, j - 1) + 1;
    }
}

• 时间复杂度：O(m×n)。其中 m 是给定网格中的行数，n 是列数。我们访问每个网格最多一次。
• 空间复杂度：O(m×n)，递归的深度最大可能是整个网格的大小，因此最大可能使用 O(m×n) 的栈空间。

BFS

class Solution {
    int[][] dirs = new int[][] { { -1, 0 }, { 1, 0 }, { 0, 1 }, { 0, -1 } };

    public int maxAreaOfIsland(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int ans = 0;

        Queue<int[]> q = new LinkedList<>();
        boolean[][] visited = new boolean[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1 && !visited[i][j]) {
                    ans = Math.max(ans, bfs(q, grid, visited, m, n, i, j));
                }
            }
        }
        return ans;
    }

    public int bfs(Queue<int[]> q, int[][] grid, boolean[][] visited, int m, int n, int i, int j) {
        int res = 0;

        q.offer(new int[] { i, j });
        visited[i][j] = true;
        res++;

        while (!q.isEmpty()) {
            int[] a = q.poll();
            int r = a[0];
            int c = a[1];

            for (int k = 0; k < 4; k++) {
                int newR = r + dirs[k][0];
                int newC = c + dirs[k][1];

                if (newR >= 0 && newR < m && newC >= 0 && newC < n && !visited[newR][newC]
                        && grid[newR][newC] == 1) {
                    // 队列里只存陆地。
                    q.offer(new int[] { newR, newC });
                    visited[newR][newC] = true;
                    res++;
                }
            }
        }
        return res;
    }
}