145. 二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

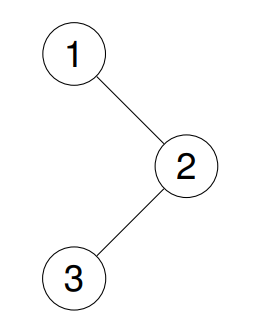
示例 1：

**输入：**root = [1,null,2,3]

输出：[3,2,1]

解释：

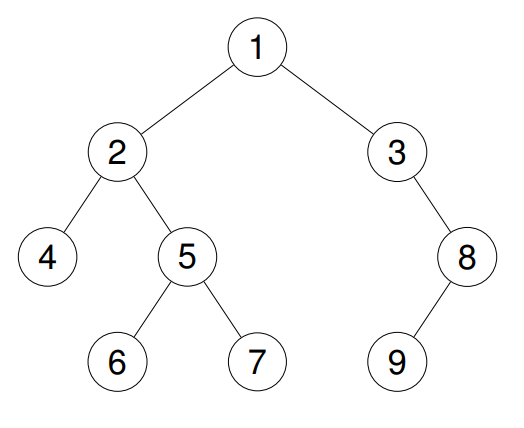
示例 2：

**输入：**root = [1,2,3,4,5,null,8,null,null,6,7,9]

输出：[4,6,7,5,2,9,8,3,1]

解释：

示例 3：

**输入：**root = []

输出：[]

示例 4：

**输入：**root = [1]

输出：[1]

提示：

• 树中节点的数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

有返回值无辅助参数的DFS，归并

class Solution {
    // 动态规划思路
    // 定义：输入一个节点，返回以该节点为根的二叉树的后序遍历结果
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new LinkedList<>();
        if (root == null) {
            return res;
        }
        
        // 后序遍历结果特点：先是左子树，接着是右子树，最后是根节点的值
        res.addAll(postorderTraversal(root.left));
        res.addAll(postorderTraversal(root.right));
        res.add(root.val);
        return res;
    }
}

• 时间复杂度：$O(n)$，其中 $n$ 是二叉树的节点数。每一个节点恰好被遍历一次。
• 空间复杂度：$O(n)$，为递归过程中栈的开销，平均情况下为 $O(\log n)$，最坏情况下树呈现链状，为 $O(n)$。

无返回值，回溯

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        postorder(root, res);
        return res;
    }

    public void postorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        postorder(root.left, res);
        postorder(root.right, res);
        res.add(root.val);
    }
}

• 时间复杂度：$O(n)$，其中 $n$ 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
• 空间复杂度：$O(n)$，为递归过程中栈的开销，平均情况下为 $O(\log n)$，最坏情况下树呈现链状，为 $O(n)$。

Morris

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        // 创建结果列表，用于存储后序遍历的节点值
        List<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;  // 如果根节点为空，直接返回空列表
        }

        // currentNode 表示当前遍历的节点，predecessor 表示当前节点的前驱节点
        TreeNode currentNode = root, predecessor = null;

        // 开始遍历树
        while (currentNode != null) {
            predecessor = currentNode.left;  // predecessor 指向 currentNode 的左子节点
            if (predecessor != null) {
                // 寻找 currentNode 节点的前驱节点（左子树中的最右节点）
                while (predecessor.right != null && predecessor.right != currentNode) {
                    predecessor = predecessor.right;
                }
                if (predecessor.right == null) {
                    // 如果前驱节点的右指针为空，将其指向 currentNode，构建线索
                    predecessor.right = currentNode;
                    // 移动 currentNode 到其左子节点，继续遍历
                    currentNode = currentNode.left;
                    // 重点
                    continue;
                } else {
                    // 如果前驱节点的右指针指向 currentNode，恢复树的原结构
                    predecessor.right = null;
                    // 将从 currentNode.left 到 currentNode 的路径（全是往右走）添加到结果中，并反转顺序。
                    // 重点。在示例2中路径是7,5,2，因为后序遍历是4,6,7,5,2
                    addPath(result, currentNode.left);
                }
            }
            // 如果没有左子树，直接移动到右子节点
            currentNode = currentNode.right;
        }
        // 最后将根节点到最右节点的路径添加到结果中，并反转顺序
        addPath(result, root);
        return result;  // 返回后序遍历的结果
    }

    public void addPath(List<Integer> result, TreeNode node) {
        List<Integer> temp = new ArrayList<>();
        while (node != null) {
            temp.add(node.val);  // 将节点值添加到临时列表
            node = node.right;  // 移动到右子节点
        }
        // 反转临时列表的顺序，并将其添加到结果中
        for (int i = temp.size() - 1; i >= 0; i--) {
            result.add(temp.get(i));
        }
    }
}

时间复杂度：O(n)，其中 n 是二叉树的节点数。没有左子树的节点只被访问一次，有左子树的节点被访问两次。

空间复杂度：O(1)。只操作已经存在的指针（树的空闲指针），因此只需要常数的额外空间。