257. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

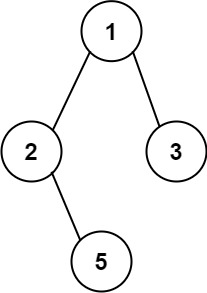
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

提示：

• 树中节点的数目在范围 [1, 100] 内
• -100 <= Node.val <= 100

无返回值有信息参数的DFS

public class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> result = new ArrayList<>();
        dfs(root, "", result);
        return result;
    }

    private void dfs(TreeNode node, String path, List<String> result) {
        // 如果当前节点为空，直接返回（不做任何操作）
        if (node == null) {
            return;
        }
        // 结束条件：如果不为空，则检查它是不是叶子节点，则添加结果并返回。在示例一中，1->2不是路径，1->2->3才是一条路径，即一定得在叶子节点结束。
        // 箭头下面如果是null，则不添加，直接返回，如果不是null，则添加node.val，如果是叶子节点，则添加完要返回，否则添加完前进。
        if (node.left == null && node.right == null) {
            // 不用新建字符串，因为path是参数。
            result.add(path + node.val);
            return;
        }
        
        // 更新当前路径信息。path是参数，不用回溯。
        path += node.val;
        // 进入左子树递归
        dfs(node.left, path + "->", result);
        // 进入右子树递归
        dfs(node.right, path + "->", result);
    }
}

• 时间复杂度： $O\left(N^2\right)$，其中 $N$ 表示节点数目。 在深度优先搜索中每个节点会被访问一次且只会被访问一次，每一次会对 path 变量进行拷贝构造，时间代价为 $O(N)$，故时间复杂度为 $O\left(N^2\right)$。
• 空间复杂度： $O\left(N^2\right)$，其中 $N$ 表示节点数目。除答案数组外我们需要考虑递归调用的栈空间。 在最坏情况下，当二叉树中每个节点只有一个孩子节点时，即整棵二叉树呈一个链状，此时递归的层数为 $N$， 此时每一层的 path 变量的空间代价的总和为 $O\left(\sum_{i=1}^N i\right)=O\left(N^2\right)$。 空间复杂度为 $O\left(N^2\right)$ 。最好情况下，当二叉树为平衡二叉树时，它的高度为 $\log N$，此时空间复杂度为 $O\left((\log N)^2\right)$。

有返回值有信息参数的DFS

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        // 如果根节点为空，返回空列表
        if (root == null) {
            return new ArrayList<>();
        }

        // 调用有返回值的 dfs 方法
        return dfs(root, "");
    }

    private List<String> dfs(TreeNode node, String path) {
        List<String> result = new ArrayList<>();

        // 如果当前节点是叶子节点，将路径添加到列表中
        if (node.left == null && node.right == null) {
            path += node.val;
            result.add(path);
        } else {
            // 如果不是叶子节点，继续递归，并添加箭头
            if (node.left != null) {
                result.addAll(dfs(node.left, path + node.val + "->"));
            }
            if (node.right != null) {
                result.addAll(dfs(node.right, path + node.val + "->"));
            }
        }

        return result;
    }
}