给定三角形3个点的坐标，在给定一个点(x,y)，判断该点是否在三角形中。

坐标值均为double型

向量叉乘

若点O在三角形内部，则沿着三角形的边逆时针走，点O一定保持在边的左侧。如图示，点在逆时针行走时，在AB，BC，CA的左侧。

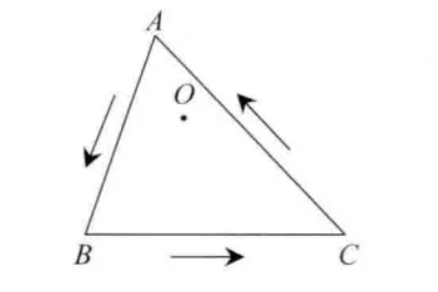
如何判断点在一个边的左侧呢？（严格来说不是左侧，而是逆时针）

可以借助向量叉乘来判断O是否在向量AB的哪一侧。若计算向量AO与向量AB的叉乘的值为正，则表示O在AB的左侧，反之为右侧。

（理解最好，理解不了也不要纠结，把叉乘公式记一下就ok）

向量 $\vec{a}$ 是 $(m, n), \vec{b}$ 是 $(p, q)$

$$\vec{a} * \vec{b}=(m * q-n * p)$$

本题的核心思路就是这样。如果要让手撕代码，题目可能没有说输入的3个点是逆时针顺序的。比如，上图中如果依次输入的是A,C,B的坐标，那就不行了。

怎么解决呢？假设依次输入的点分别是p1,p2,p3。

我们判断若p3在 $\vec{p_1p_2}$ 的右侧，则表示输入的点的顺序是顺时针的，即A,C,B式的输入，将p2,p3调换位置即可保证顺序是逆时针。

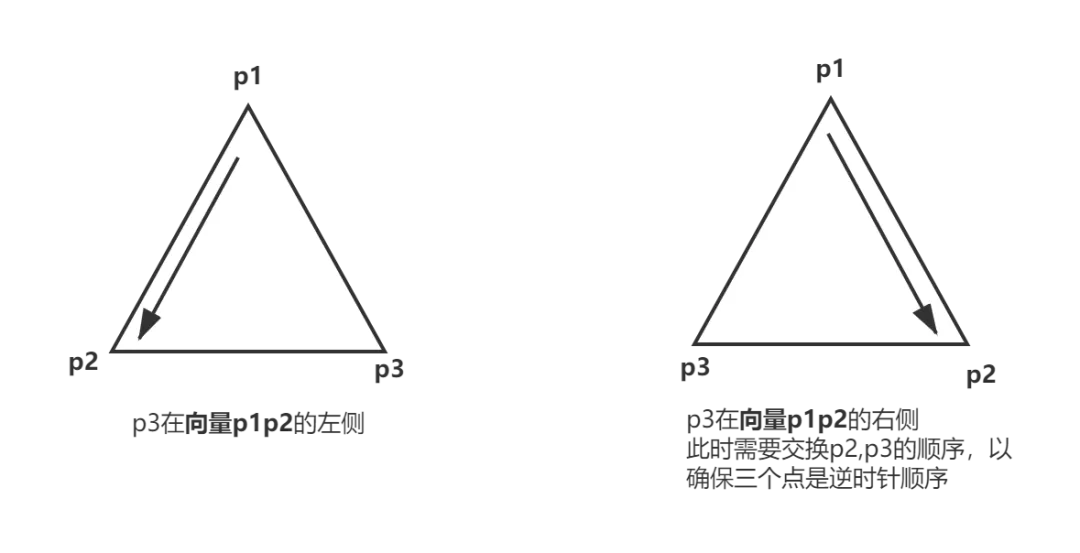
详情可以看代码。

参考代码

import java.util.Scanner;

class Point {
    double x;
    double y;

    // 构造函数
    Point(double x, double y) {
        this.x = x;
        this.y = y;
    }
}

public class Solution {
    // 计算叉乘
    public static double product(Point p1, Point p2, Point p3) {
        // 计算向量 p1p2 和 p1p3 的叉乘
        return (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x);
    }

    // 判断点 o 是否在三角形 p1p2p3 内部
    public static boolean isInTriangle(Point p1, Point p2, Point p3, Point o) {
        // 保证 p1, p2, p3 是逆时针顺序。右手定则。逆时针时叉乘为正，顺时针为负。
        if (product(p1, p2, p3) < 0) {
            // 如果不是逆时针，交换 p2 和 p3 的顺序
            return isInTriangle(p1, p3, p2, o);
        }

        // 判断点 o 是否在三角形内，通过检查三个子三角形的叉乘是否为正
        return product(p1, p2, o) > 0 && product(p2, p3, o) > 0 && product(p3, p1, o) > 0;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        // 读取三角形的三个顶点
        System.out.println("请输入三角形三个顶点坐标：");
        Point p1 = new Point(sc.nextDouble(), sc.nextDouble());
        Point p2 = new Point(sc.nextDouble(), sc.nextDouble());
        Point p3 = new Point(sc.nextDouble(), sc.nextDouble());

        // 读取待判断的点
        System.out.println("请输入待判断的点坐标：");
        Point o = new Point(sc.nextDouble(), sc.nextDouble());

        // 判断点 o 是否在三角形内
        boolean flag = isInTriangle(p1, p2, p3, o);

        // 输出结果
        if (flag) {
            System.out.println("Yes");
        } else {
            System.out.println("No");
        }

        sc.close();
    }
}