景真

外观

二叉树的直径

约 870 字大约 3 分钟

DFS后序

2025-02-25

543. 二叉树的直径

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

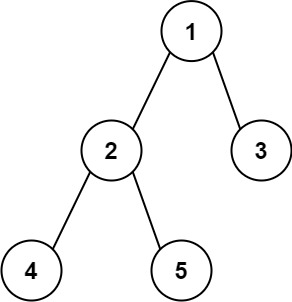
img.png

输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

提示：

  • 树中节点数目在范围 [1, 10^4] 内
  • -100 <= Node.val <= 100

DFS-递归-后序遍历

左子树的深度加右子树的深度再加一（根节点）即最长直径中的节点数，题目要求的是边数，所以要减一。

注意递归函数返回的是以该节点为根的子树的深度

注意本题和310最小高度树中寻找最长路径的区别，310中是图，所以可以从叶子节点走到另一个叶子节点，但是本题是树，只能往下走，即只能从根节点走到叶子节点。

注意最长路径可能不经过根节点 root 。

计算以每个节点为根节点的最长路径的长度。

如何计算呢？只需计算左右子树的深度，把它们相加再加1再减1即可。

因此我们的递归方法就是计算以当前节点为根节点的树的深度，在后序部分计算以当前节点为根节点（即经过当前节点）的最长路径的长度。

class Solution {
    int ans;
    public int diameterOfBinaryTree(TreeNode root) {
        ans = 1;
        depth(root);
        // ans指的是路径上节点的个数，而题目中说长度是边数，所以要减一。
        return ans - 1;
    }
    
    // 注意depth计算的是以该节点为根的子树的最大深度，即节点个数，不是直径！由它可以计算出直径。递归函数应该选择解决问题的最小模块。
    public int depth(TreeNode node) {
        if (node == null) {
            return 0; // 访问到空节点了，返回0
        }
        
        int L = depth(node.left); // 左儿子为根的子树的深度
        int R = depth(node.right); // 右儿子为根的子树的深度
        // 每轮都要计算直径，因为直径的最大值的分布没有规律，尤其是没有递归性，不知道在哪次递归中出现最大值。重点。
        ans = Math.max(ans, L+R+1); // 计算d_node即L+R+1 并更新ans。注意这里要加1不能加2，因为ans是节点个数，depth返回值也是节点的个数，不是边的个数。
        return Math.max(L, R) + 1; // 返回该节点为根的子树的深度，即节点个数
    }
}
  • 时间复杂度：O(N)O(N) ，其中 NN 为二叉树的节点数，即遍历一棵二叉树的时间复杂度，每个结点只被访问一次。
  • 空间复杂度：O(Height)O(Height)，其中 Height 为二叉树的高度。由于递归函数在递归过程中需要为每一层递归函数分配栈空间， 所以这里需要额外的空间且该空间取决于递归的深度，而递归的深度显然为二叉树的高度，并且每次递归调用的函数里又只用了常数个变量，所以所需空间复杂度为 O(Height)O(Height) 。