701. 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

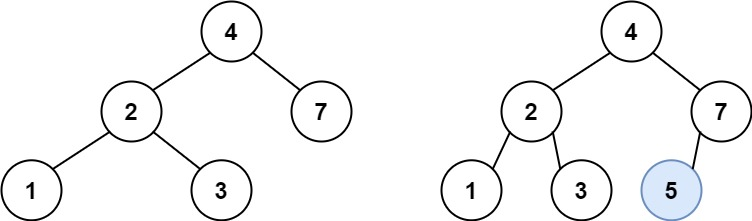
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：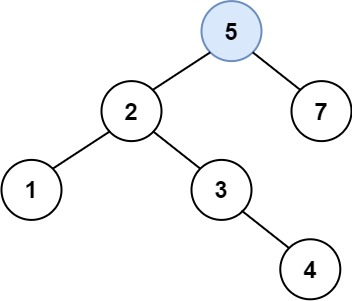

示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

提示：

• 树中的节点数将在 [0, 10^4]的范围内。
• -10^8 <= Node.val <= 10^8
• 所有值 Node.val 是 独一无二 的。
• -10^8 <= val <= 10^8
• 保证 val 在原始BST中不存在。

插入操作是指构建父子关系。因此要有root.left=node这种操作。

递归

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        // 找到空位置插入新节点
        if (root == null) return new TreeNode(val);
        
        // if (root.val == val)
        // BST 中一般不会插入已存在元素
        if (root.val < val)
            // 注意这里不是return，而是构建右子树！因为返回值是构建好的子树的根节点。
            root.right = insertIntoBST(root.right, val);
        if (root.val > val)
            root.left = insertIntoBST(root.left, val);
        // 题目说val不存在于树中，因此没必要处理相等的情况。
        return root;
    }
}

迭代+二分，为空就插入，不为空就前进。

如果 root 是空，则新建树节点作为根节点返回即可。否则二分，如果当前节点的值大于要插入的值，则遍历左子树，直到找到一个空节点，插入即可。否则遍历右子树。

有多种插入方式，我们选择在空节点插入而不是在两个节点中间插入。

先确定方向，确定方向后，该方向的子节点不为空就前进，为空就插入。

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        TreeNode node = new TreeNode(val); // 创建一个新的树节点
        if (root == null) {
            return node; // 如果根节点为空，直接返回新节点作为根节点
        }

        TreeNode cur = root; // 记录根节点，接下来要前进，会改变root的值。类似虚拟节点和构建节点。
        while (true) {
            if (cur.val > val) {
                // 如果当前节点的值大于要插入的值，则需要把val插入到cur的左子树中
                if (cur.left == null) {
                    cur.left = node; // 如果左子节点为空，将新节点插入左子节点。重点。
                    break; // 插入后跳出循环
                }
                cur = cur.left; // 移动到左子节点继续遍历
            } else {
                // 如果当前节点的值小于要插入的值，则需要把val插入到cur的右子树中
                if (cur.right == null) {
                    cur.right = node; // 如果右子节点为空，将新节点插入右子节点
                    break; // 插入后跳出循环
                }
                cur = cur.right; // 移动到右子节点继续遍历
            }
        }
        return root; // 返回根节点
    }
}

注意不能这样写

        while (true) {
            if (cur == null) {
                cur = node;
                break;
            }
            if (cur.val > val) {
                cur = cur.left; // 移动到左子节点继续遍历
            } else {
                cur = cur.right; // 移动到右子节点继续遍历
            }
        }

因为我们遇到null时，不知道cur是哪个节点的子节点。