1035. 不相交的线

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足：

• nums1[i] == nums2[j]
• 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

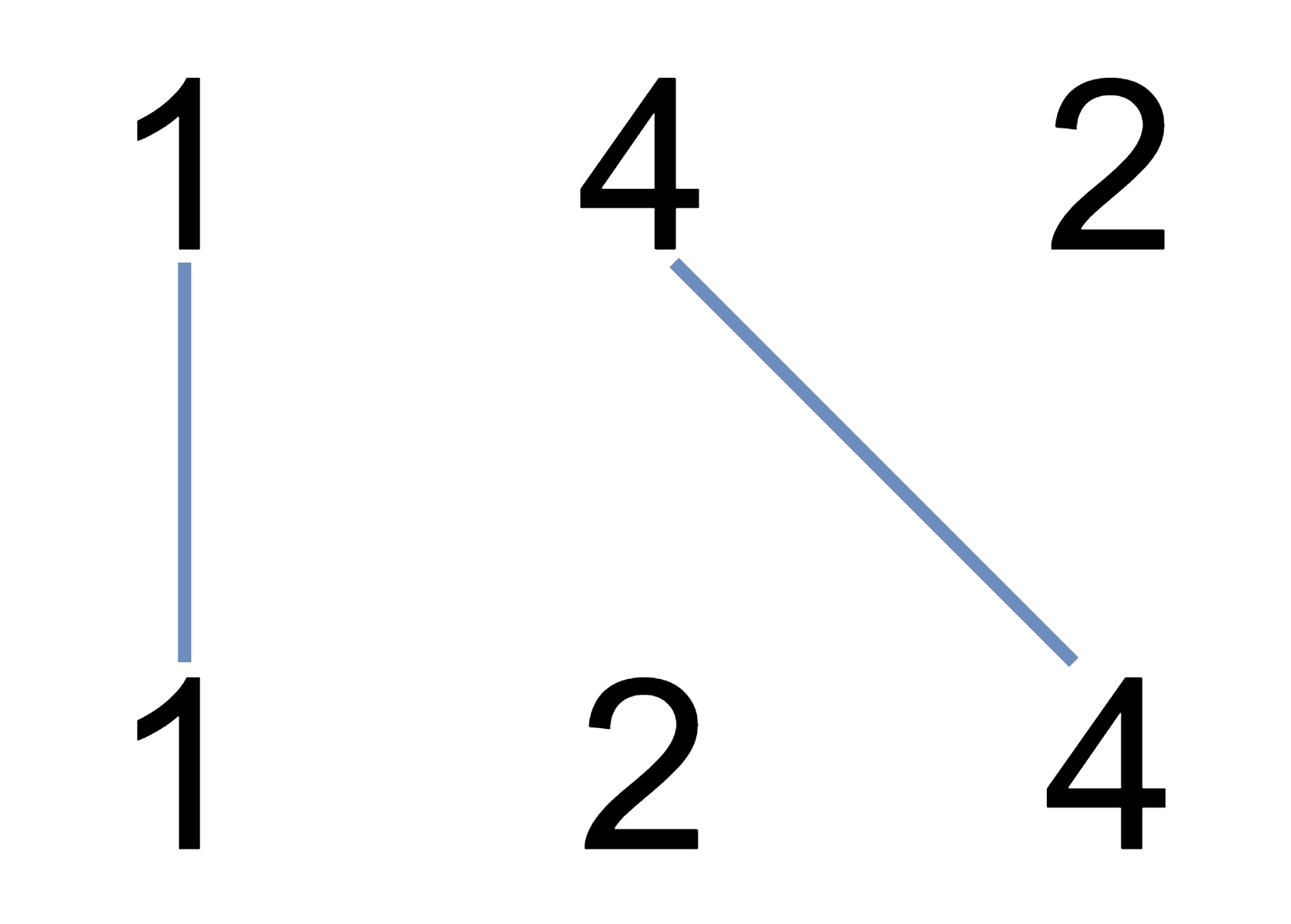
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

示例 3：

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

提示：

• 1 <= nums1.length, nums2.length <= 500
• 1 <= nums1[i], nums2[j] <= 2000

动态规划-数组递推

本质是最长公共子序列问题。

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int m = nums1.length, n = nums2.length; // 获取 nums1 和 nums2 的长度
        // 定义 dp 数组，dp[i][j] 表示 nums1[0..i-1] 和 nums2[0..j-1] 的最长不相交子序列的长度,i和j指的是前i个和前j个元素。
        int[][] dp = new int[m + 1][n + 1];

        // 遍历 nums1 的每个元素
        for (int i = 1; i <= m; i++) {
            int num1 = nums1[i - 1]; // 获取 nums1 中的第 i 个元素
            // 遍历 nums2 的每个元素
            for (int j = 1; j <= n; j++) {
                int num2 = nums2[j - 1]; // 获取 nums2 中的第 j 个元素
                if (num1 == num2) {
                    // 如果 nums1[i-1] 和 nums2[j-1] 相同，则它们可以构成一条不相交的线
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    // 否则，取 dp[i-1][j] 和 dp[i][j-1] 的较大值。重点。
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        // 返回 nums1 和 nums2 的最长不相交子序列的长度
        return dp[m][n];
    }
}

时间复杂度O(mn)，空间复杂度O(mn)

滚动更新

用两个数组而不是一个变量+一个数组来进行滚动更新。

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int m = nums1.length, n = nums2.length;
        // 定义两个一维数组，prevRow 表示上一行，currentRow 表示当前行
        int[] prevRow = new int[n + 1];
        int[] currentRow = new int[n + 1];

        // 遍历 nums1 的每个元素
        for (int i = 1; i <= m; i++) {
            int num1 = nums1[i - 1]; // 获取 nums1 中的第 i 个元素

            // 遍历 nums2 的每个元素
            for (int j = 1; j <= n; j++) {
                int num2 = nums2[j - 1]; // 获取 nums2 中的第 j 个元素
                
                if (num1 == num2) {
                    // 如果 nums1[i-1] 和 nums2[j-1] 相同，则可以构成一条不相交的线
                    currentRow[j] = prevRow[j - 1] + 1;
                } else {
                    // 否则，取 prevRow[j] 和 currentRow[j-1] 的较大值
                    currentRow[j] = Math.max(prevRow[j], currentRow[j - 1]);
                }
            }

            // 将当前行变为上一行，准备进入下一次循环。重点。
            // Arrays.copyOfRange 是替代 System.arraycopy 的一个方法，但它会返回一个新的数组。
            // System.arraycopy 直接在现有数组中进行复制，适用于复制到已分配的数组中。System.arraycopy 十分高效。
            // prevRow = Arrays.copyOfRange(currentRow, 0, n + 1);
            System.arraycopy(currentRow, 0, prevRow, 0, n + 1);
        }

        // 返回 nums1 和 nums2 的最长不相交子序列的长度
        return currentRow[n];
    }
}