101. 对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

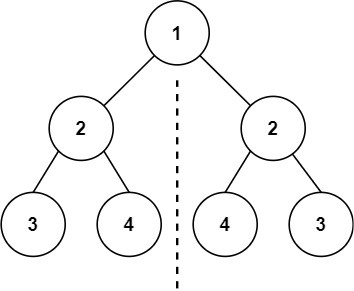
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

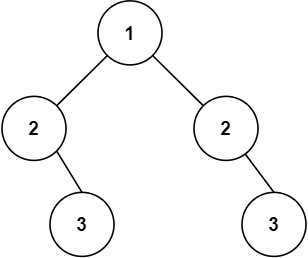
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

DFS-归并，有返回值无信息参数的DFS，无需检查叶子节点

先检查左右子节点是否相等，如果相等，再检查左节点的左子树和右节点的右子树是否相等，左节点的右子树和右节点的左子树是否相等，因为要满足镜像对称条件。

DFS：特殊条件或结束条件，操作当前节点，操作子节点。

BFS：出队、操作出队的节点、入队子节点。

注意我们是在遍历两棵树不是一棵树。因此参数是两个节点。

class Solution {
    public boolean isSymmetric(TreeNode root) {
        // 特殊条件，注意是返回true
        if (root == null) return true;
        // 检查两棵子树是否对称
        return check(root.left, root.right);
    }

    // 定义：判断输入的两棵树是否是镜像对称的
    boolean check(TreeNode left, TreeNode right) {
        // 结束条件。重点。
        if (left == null || right == null) {
            return left == right;
        }
        // 两个根节点需要相同。注意这里检查的是val，不是节点本身！
        if (left.val != right.val) return false;
        // 左右子树也需要镜像对称。重点。
        return check(left.right, right.left) && check(left.left, right.right);
    }
}

假设树上一共 n 个节点。

• 时间复杂度：这里遍历了这棵树，渐进时间复杂度为 O(n)。
• 空间复杂度：O(h)，这里的空间复杂度和递归使用的栈空间有关，这里递归层数不超过 n，故渐进空间复杂度为 O(n)。

BFS

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) return true;

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root.left);
        queue.offer(root.right);

        while (!queue.isEmpty()) {
            TreeNode left = queue.poll();
            TreeNode right = queue.poll();

            if (left == null || right == null) {
                if (left == null && right == null) {
                    // 重点
                    continue;
                }
                return false;
            }
            if (left.val != right.val) {
                return false;
            }

            // 注意入队顺序
            queue.offer(left.left);
            queue.offer(right.right);
            queue.offer(left.right);
            queue.offer(right.left);
        }
        
        return true;
    }
}

• 时间复杂度：O(n)，同方法一。
• 空间复杂度：这里需要用一个队列来维护节点，每个节点最多进队一次，出队一次，队列中最多不会超过 (n+1)/2 个点，故渐进空间复杂度为 O(n)。