135. 分发糖果

n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。

你需要按照以下要求，给这些孩子分发糖果：

• 每个孩子至少分配到 1 个糖果。
• 相邻两个孩子评分更高的孩子会获得更多的糖果。

请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。

示例 1：

输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。

示例 2：

输入：ratings = [1,2,2]
输出：4
解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
     第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

提示：

• n == ratings.length
• 1 <= n <= 2 * 10^4
• 0 <= ratings[i] <= 2 * 10^4

两次遍历+贪心。

1. 双向约束：本质上，这是一个双向约束问题。左到右和右到左的规则同时存在，这两个方向的条件需要同时满足。因此，通过分别计算每个方向的最优值， 然后在每个位置取最大值，确保两个方向的规则都得到满足。
2. 局部最优推导全局最优：代码的精髓在于通过两次单向的线性扫描，分别满足两个方向的局部最优条件，然后结合这两个局部最优条件推导出全局最优解。
3. 渐进式分配：这个方法背后的直觉是，从一个方向扫描时，只要当前孩子比前一个孩子的评分高，我们就增加他的糖果数， 保持这种关系是最优的。同理，从另一个方向扫描时也一样。

我们可以将「相邻的孩子中，评分高的孩子必须获得更多的糖果」这句话拆分为两个规则，分别处理。

• 左规则: 当 ratings [i-1]< ratings[i] 时， $i$ 号学生的糖果数量将比 $i-1$ 号孩子的糖果数量多。
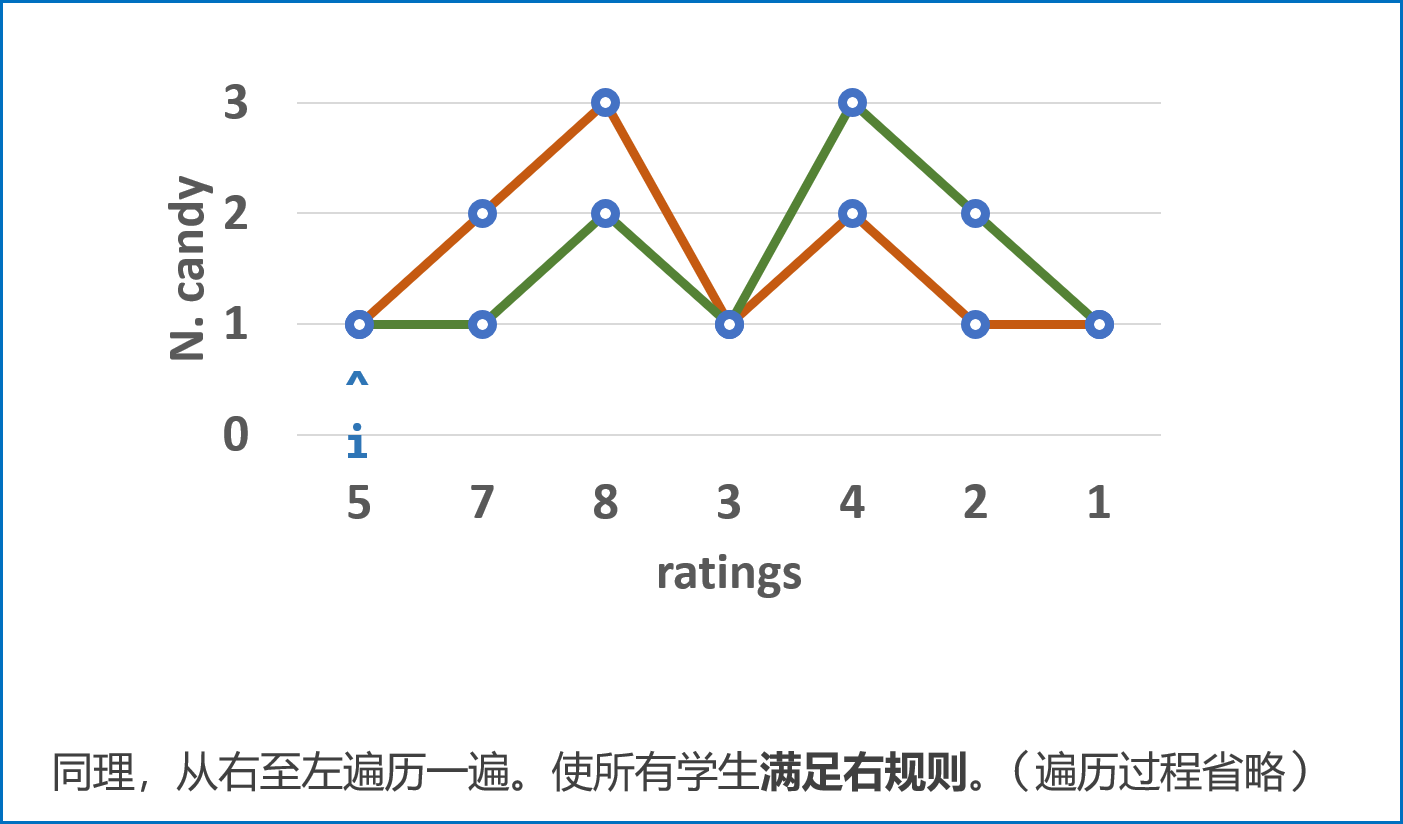
• 右规则：当 ratings[i] > ratings[i+1]时， $i$ 号学生的糖果数量将比 $i+1$ 号孩子的糖果数量多。

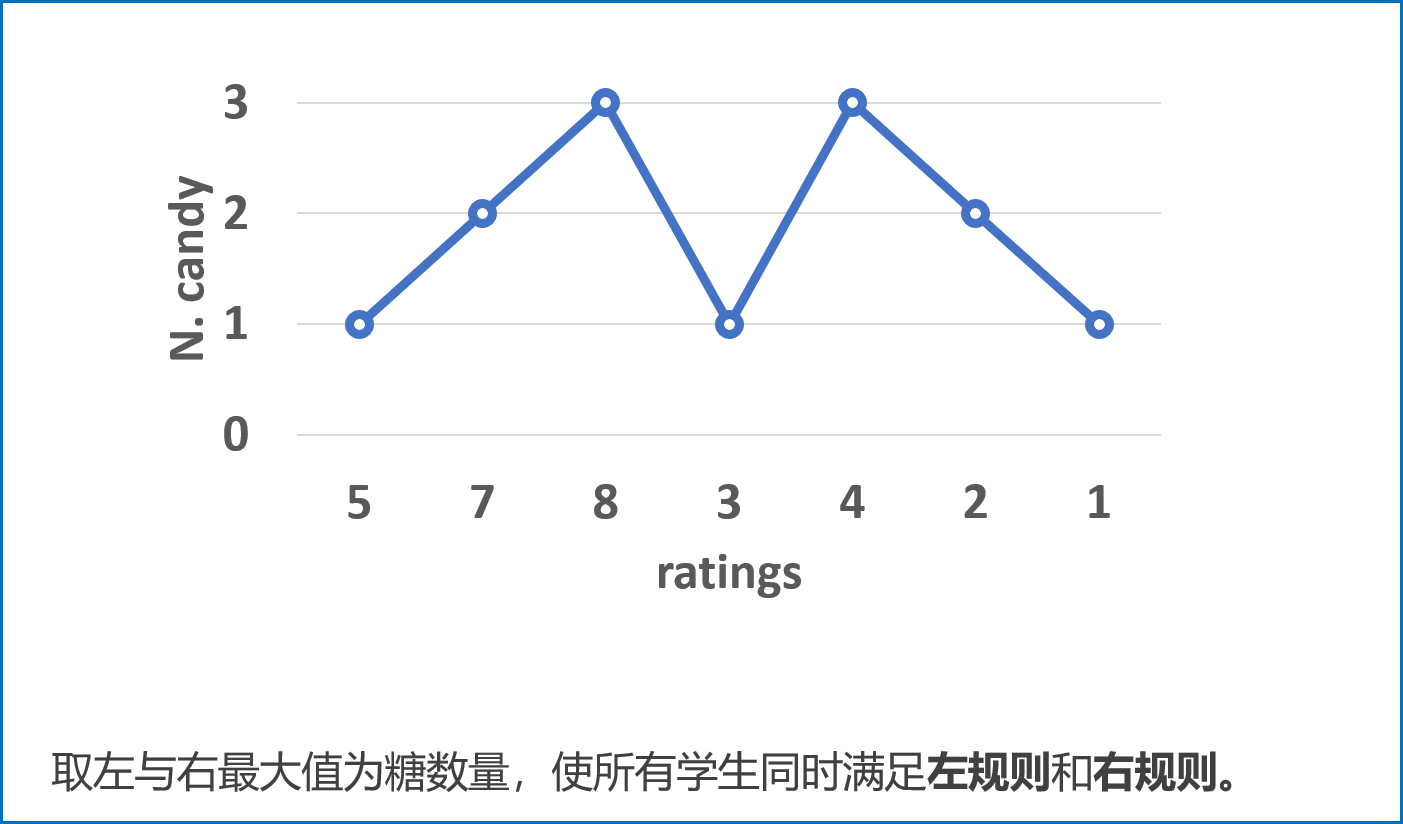
我们遍历该数组两次，处理出每一个学生分别满足左规则或右规则时，最少需要被分得的糖果数量。每个人最终分得的糖果数量即为这两个数量的最大值。

具体地，以左规则为例：我们从左到右遍历该数组，假设当前遍历到位置 $i$ ，如果有 ratings $[i-$ $1]<$ ratings $[i]$ 那么 $i$ 号学生的糖果数量将比 $i-1$ 号孩子的糖果数量多，我们令 left $[i]=l$ efft $[i-$ $1]+1$ 即可，否则我们令 left $[i]=1$ 。

在实际代码中，我们先计算出左规则 left 数组，在计算右规则的时候只需要用单个变量记录当前位置的右规则，同时计算答案即可。

从左到右遍历时，如果递增，则加一，否则直接降为1，因此递减序列中分不出大小。从右到左遍历时在前一步的基础上分清递减序列的大小。

类似最长有效括号

class Solution {
    public int candy(int[] ratings) {
        int n = ratings.length;
        if (n == 0) return 0;

        // 初始化两个数组，长度均为 n
        // left[i] 表示在满足从左到右的规则下，第 i 个孩子至少需要多少糖果。
        int[] left = new int[n];
        // right[i] 表示在满足从右到左的规则下，第 i 个孩子至少需要多少糖果。
        int[] right = new int[n];

        // 初始化每个孩子至少有一个糖果
        Arrays.fill(left, 1);
        Arrays.fill(right, 1);

        // 从左到右遍历，更新 left 数组
        for (int i = 1; i < n; i++) {
            if (ratings[i] > ratings[i - 1]) {
                left[i] = left[i - 1] + 1;
            }
        }
        // 从右到左遍历，更新 right 数组
        for (int i = n - 2; i >= 0; i--) {
            if (ratings[i] > ratings[i + 1]) {
                right[i] = right[i + 1] + 1;
            }
        }

        // 计算总糖果数，取两个数组中的最大值
        int totalCandy = 0;
        for (int i = 0; i < n; i++) {
            totalCandy += Math.max(left[i], right[i]);
        }
        return totalCandy;
    }
}

空间优化，在计算右规则的时候只需要用单个变量记录当前位置的右规则，同时计算答案即可。left数组不能优化，因为在从右往左遍历时需要用到left[i]取最值。

class Solution {
    public int candy(int[] ratings) {
        int n = ratings.length; // 获取学生的数量
        int[] left = new int[n]; // 创建数组用于记录从左到右的分配糖果数量
        
        // 第一次遍历，从左到右分配糖果
        for (int i = 0; i < n; i++) {
            // 如果当前学生的评分高于前一个学生，则当前学生的糖果数量比前一个多一个
            if (i > 0 && ratings[i] > ratings[i - 1]) {
                left[i] = left[i - 1] + 1;
            } else {
                // 否则，当前学生的糖果数量至少为1
                left[i] = 1;
            }
        }

        int right = 0; // 用于记录从右到左的当前学生的糖果数量
        int ret = 0; // 最终返回的总糖果数量

        // 第二次遍历，从右到左分配糖果，同时计算总糖果数量
        for (int i = n - 1; i >= 0; i--) {
            // 如果当前学生的评分高于后一个学生，则当前学生的糖果数量比后一个多一个
            if (i < n - 1 && ratings[i] > ratings[i + 1]) {
                right++;
            } else {
                // 否则，当前学生的糖果数量至少为1。最右边的学生的糖果数是1而不是left[n-1]（可能比1大），下面还要取最大值，所以没关系。
                // right一开始是1，如果倒数第二个比最后一个大，那么right变为2，即倒数第二个学生的糖果数是2。
                right = 1;
            }
            // 累加当前学生的糖果数量，取左右两侧的最大值
            ret += Math.max(left[i], right);
        }

        return ret; // 返回最终的总糖果数量
    }
}

• 时间复杂度：O(n)，其中 n 是孩子的数量。我们需要遍历两次数组以分别计算满足左规则或右规则的最少糖果数量。
• 空间复杂度：O(n)，其中 n 是孩子的数量。我们需要保存所有的左规则对应的糖果数量。