LCR 143. 子结构判断

给定两棵二叉树 tree1 和 tree2，判断 tree2 是否与以 tree1 的某个节点为根的子树具有 相同的结构和节点值 。

注意，空树 不会与以 tree1 的某个节点为根的子树具有 相同的结构和节点值 。

示例 1：

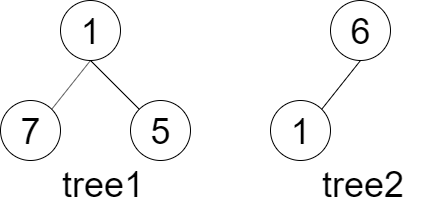
输入：tree1 = [1,7,5], tree2 = [6,1]
输出：false
解释：tree2 与 tree1 的一个子树没有相同的结构和节点值。

示例 2：

输入：tree1 = [3,6,7,1,8], tree2 = [6,1]
输出：true
解释：tree2 与 tree1 的一个子树拥有相同的结构和节点值。即 6 - > 1。

提示：

0 <= 节点个数 <= 10000

递归-自顶向下

class Solution {
    String target;
    boolean found = false;

    // 这个函数用「遍历」的思维模式理解，遍历二叉树 A 的所有节点
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        // 题目说空树不会与以 `tree1` 的某个节点为根的子树具有相同的结构和节点值。
        if (A == null || B == null) {
            return false;
        }
        
        // 对于树 A 中的一个节点：
        // 1. A 可以作为根节点尝试去匹配树 B
        if (compareTree(A, B)) {
            return true;
        }
        // 2. 如果 A.val != B.val，就不要去匹配树 B 了。注意，固定用B与A的子树比较。
        // 注意最坏情况是遍历A的所有节点，而不是每次一定遍历一半！所以时间复杂度不是对数。
        return isSubStructure(A.left, B) || isSubStructure(A.right, B);
    }

    // 这个函数用「分解问题」的思路理解
    // 定义：输入两个根节点，返回从 rootA 开始是否可以完全匹配 rootB 树上的所有节点
    boolean compareTree(TreeNode rootA, TreeNode rootB) {
        // 结束条件：rootB为空，rootA随便。注意这里的rootB==null指的是前进到B的空节点，不是指一开始rootB就是空，
        // isSubStructure中有判空，所以一开始rootB一定不为空。
        if (rootB == null) {
            return true;
        }
        // 结束条件：rootA为空且rootB不为空
        if (rootA == null) {
            return false;
        }
        // 结束条件：rootA和rootB都不为空且不相等
        if (rootA.val != rootB.val) {
            return false;
        }

        // rootA 的值和 rootB 的值匹配完成，去匹配子树的节点
        return compareTree(rootA.left, rootB.left) && compareTree(rootA.right, rootB.right);
    }
}

• 时间复杂度 O(MN)：其中 M，N 分别为树 A 和 树 B 的节点数量；先序遍历树 A 占用 O(M)，每次调用 compareTree(A, B) 判断占用 O(N) 。
• 空间复杂度 O(M)：当树 A 和树 B 都退化为链表时，递归调用深度最大。当 M≤N 时，遍历树 A 与递归判断的总递归深度为 M ； 当 M>N 时，最差情况为遍历至树 A 的叶节点，此时总递归深度为 M。

注意就算isSubStructure每次都执行一次compareTree，递归栈也是M，不是M^2，因为compareTree返回后递归栈会被销毁，下次运行的时候再创建。

能不能用备忘录优化？可以，但比较麻烦，因为正常来说备忘录是哈希表，哈希表的键是节点的值，值是true或false，但是二叉树中可能有重复的节点值。