96. 不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

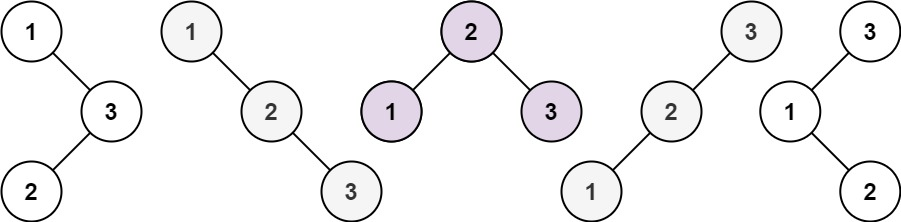
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：

• 1 <= n <= 19

动态规划-数组递推

以根节点分类

根据G(0)、G(1)算G(2)，根据G(0),G(1),G(2)算G(3)，……一直算到G(n)

• 假设 $n$ 个节点存在二叉排序树的个数是 $G(n)$，令 $f(i)$ 为以 $i$ 为根的二叉搜索树的个数，则

$$G(n)=f(1)+f(2)+f(3)+f(4)+\dots+f(n)$$

• 当 i 为根节点时，其左子树节点个数为 $i-1$ 个，右子树节点为 $n-i$，则

$$f(i)=G(i-1) * G(n-i)$$

• 综合两个公式可以得到 卡特兰数 公式

$$G(n)=G(0) * G(n-1)+G(1) *(n-2)+\dots+G(n-1) * G(0)$$

对于边界情况，当序列长度为 1 (只有根) 或为 0 (空树) 时，只有一种情况，即：

$$G(0)=1, G(1)=1$$

class Solution {
    public int numTrees(int n) {
        int[] G = new int[n + 1];
        G[0] = 1;
        G[1] = 1;

        // 根据G(0)、G(1)算G(2)，根据G(0),G(1),G(2)算G(3)，……一直算到G(n)。
        // G(i) 表示 i 个节点组成的二叉搜索树的个数。
        for (int i = 2; i <= n; ++i) {
            // f(j) 表示以 j 为根的二叉搜索树的个数。假设节点的索引从1开始。
            for (int j = 1; j <= i; ++j) {
                // G[2]=f(1)+f(2), f(j)=G[j-1]*G[i-j]
                // 以 j 为根节点的话，左子树有 j-1 个节点（[1...j-1]），右子树有 i-j 个节点（[j+1...n]）。
                G[i] += G[j - 1] * G[i - j];
            }
        }
        
        return G[n];
    }
}

• 时间复杂度：$O\left(n^2\right)$ ，其中 $n$ 表示二叉搜索树的节点个数。$G(n)$ 函数一共有 $n$ 个值需要求解，每次求解需要 $O(n)$ 的时间复杂度， 因此总时间复杂度为 $O\left(n^2\right)$ 。
• 空间复杂度：$O(n)$ 。我们需要 $O(n)$ 的空间存储 $G$ 数组。

数学-Catalan数

事实上我们在方法一中推导出的 G(n) 函数的值在数学上被称为卡塔兰数$C_n$。 卡塔兰数更便于计算的定义如下:

$$C_0=1, \quad C_{n+1}=\frac{2(2 n+1)}{n+2} C_n$$

class Solution {
    public int numTrees(int n) {
        // 提示：我们在这里需要用 long 类型防止计算过程中的溢出
        long C = 1;
        for (int i = 0; i < n; ++i) {
            C = C * 2 * (2 * i + 1) / (i + 2);
        }
        return (int) C;
    }
}

• 时间复杂度 : O(n)，其中 n 表示二叉搜索树的节点个数。我们只需要循环遍历一次即可。
• 空间复杂度 : O(1)。我们只需要常数空间存放若干变量。

动态规划-递归+备忘录，有返回值有信息参数的DFS

初始化备忘录的值为 0，计算从 1 到 n 的不同二叉搜索树的数量。当 lo 大于等于 hi 时，返回 1，表示空树也是一种有效的二叉搜索树，否则，枚举所有可能的根节点。递归计算左子树的数量，递归计算右子树的数量，当前树的数量是左右子树数量的乘积。

为什么需要备忘录？假设n=5，则count(2, 5)需要计算count(4,5)，count(3, 5)也需要计算count(4, 5)。

class Solution {
    // 备忘录，用于存储已经计算过的子问题结果
    int[][] memo;

    int numTrees(int n) {
        // 初始化备忘录的值为 0
        memo = new int[n + 1][n + 1];
        // 计算从 1 到 n 的不同二叉搜索树的数量
        return count(1, n);
    }

    // 递归计算从 lo 到 hi 之间的不同二叉搜索树的数量
    int count(int lo, int hi) {
        // 当 lo 大于等于 hi 时，返回 1，表示空树也是一种有效的二叉搜索树
        if (lo >= hi) return 1; // > 或者 >= 都可以
        // 查备忘录，如果已经计算过，直接返回结果
        if (memo[lo][hi] != 0) {
            return memo[lo][hi];
        }

        int res = 0; // 存储结果
        // 枚举所有可能的根节点
        for (int mid = lo; mid <= hi; mid++) {
            // 递归计算左子树的数量。因为数组是升序的，所以左子树的数据一定都小于根节点。右子树同理。从而构建出来的二叉树一定是二叉搜索树。
            int left = count(lo, mid - 1);
            // 递归计算右子树的数量
            int right = count(mid + 1, hi);
            // 当前树的数量是左右子树数量的乘积。重点。
            res += left * right;
        }
        
        // 将结果存入备忘录
        memo[lo][hi] = res;
        return res; // 返回结果
    }
}

不使用备忘录的时间复杂度接近 O(4^n / n^{3/2})，这是卡塔兰数的增长率。因为递归树中每一个可能的子问题都会被计算多次，而这些子问题的数量正是卡塔兰数。

递归调用的深度与树的高度有关。在最坏情况下，递归栈的最大深度等于 n，即当所有节点都在一条路径上时（类似链表的情况）。