103. 二叉树的锯齿形层序遍历

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

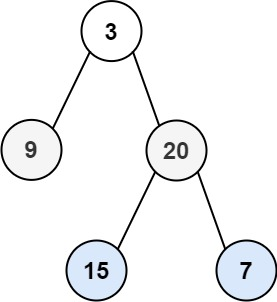
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 [0, 2000] 内
• -100 <= Node.val <= 100

层序遍历

类似102. 二叉树的层序遍历，布尔变量 flag 控制遍历方向，如果是从右向左遍历，则从队头进入记录队列，遍历队列的入队方向不变。

注意，出队后再加入层列表，不是入队前加入。

这题和 102. 二叉树的层序遍历 几乎是一样的， 只要用一个布尔变量 flag 控制遍历方向即可。

class Solution {
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> res = new LinkedList<>();
        if (root == null) {
            return res;
        }

        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        // 为 true 时向右，false 时向左
        boolean flag = true;

        // while 循环控制从上向下一层层遍历
        // 层序遍历是循环，BFS是函数。它们的队列都是辅助，存中间结果的。
        while (!q.isEmpty()) {
            int sz = q.size();
            
            // 记录这一层的节点值
            List<Integer> level = new LinkedList<>();
            // for 循环控制每一层从左向右遍历
            for (int i = 0; i < sz; i++) {
                TreeNode cur = q.poll();
                
                // 实现 z 字形遍历
                if (flag) {
                    level.addLast(cur.val);
                } else {
                    level.addFirst(cur.val);
                }
                
                // 入队子节点时总是从左到右入队，但是出队后记录到level中时是锯齿型记录到链表中。
                if (cur.left != null)
                    q.offer(cur.left);
                if (cur.right != null)
                    q.offer(cur.right);
            }
            
            // 切换方向
            flag = !flag;
            res.add(level);
        }
        return res;
    }
}

记树上所有节点的个数为 n。

• 时间复杂度：每个点进队出队各一次，故渐进时间复杂度为 O(n)。
• 空间复杂度：队列中元素的个数不超过 n 个，故渐进空间复杂度为 O(n)。

无返回值有信息参数的DFS

用一个变量记录遍历的层数，即递归的层数，从零开始，偶数层从左到右，把节点加到对应队列（索引等于递归的层数）的末尾，奇数层从右到左，把节点加到对应队列的队首。

class Solution {
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        dfs(root, 0);
        return res;
    }

    private void dfs(TreeNode cur, int level) {
        if (cur == null)
            return;
        
        // 如果res.size() <= level说明下一层的集合还没创建，所以要先创建下一层的集合，不然下面的res.get(level)就会出错
        if (res.size() <= level) {
            List<Integer> newLevel = new LinkedList<>();
            res.add(newLevel);
        }
        // 这里默认根节点是第0层，偶数层相当于从左往右遍历，
        // 所以要添加到集合的末尾，如果是奇数层相当于从右往左遍历，
        // 要把数据添加到集合的开头
        if (level % 2 == 0)
            res.get(level).add(cur.val);
        else
            res.get(level).add(0, cur.val); // 注意api
        
        // 分别遍历左右两个子节点，到下一层了，所以层数要加1
        dfs(cur.left, level + 1);
        dfs(cur.right, level + 1);
    }
}

代码的时间复杂度主要由递归遍历二叉树的操作决定。代码中，每个节点都被访问了一次，并且在每个节点上进行了常数时间的操作（添加节点值到列表中）。

1. 遍历节点：
   • 递归函数 dfs 对每个节点访问一次，因此访问节点的总次数是 O(n)，其中 n 是二叉树中的节点数。
2. 操作分析：
   • 对于每个节点，首先检查是否为 null，然后检查并添加当前节点值到结果列表中，这些操作都是常数时间 O(1)。

空间复杂度包括以下几个方面：

1. 递归调用栈：
   • 递归深度最大为二叉树的高度 h。在最坏情况下，树是完全不平衡的，树的高度为 n，此时递归调用栈的空间复杂度为 O(n)。
   • 在最好情况下，树是完全平衡的，树的高度为 log(n)，此时递归调用栈的空间复杂度为 O(log(n))。
2. 结果列表 res：
   • 结果列表 res 存储了所有节点的值，空间复杂度为 O(n)，因为每个节点的值都需要存储在列表中。