景真

外观

二叉搜索树中的搜索

约 1025 字大约 3 分钟

二分迭代递归

2025-02-25

700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

示例 1:

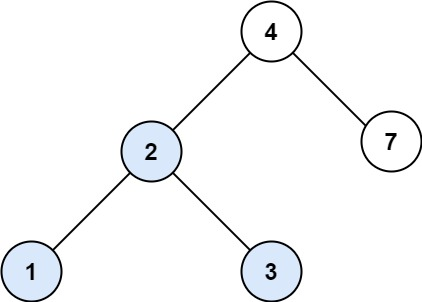
img.png

输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

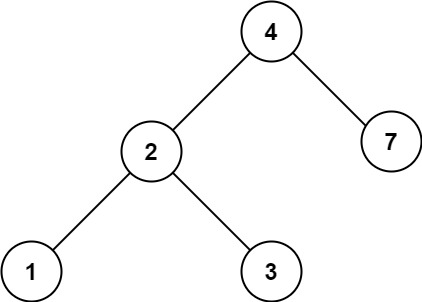
img.png

输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

  • 树中节点数在 [1, 5000] 范围内
  • 1 <= Node.val <= 107
  • root 是二叉搜索树
  • 1 <= val <= 107

递归+二分

后序，先处理左右子树（即根节点的值不等于目标值的情况），再处理根节点。

如果没有节点的值等于target，那么只能小于或大于，从而会一直前进，最终走到null，返回。如果有节点的值等于target，就会提前返回，不会走到null。

class Solution {
    // 主函数，用于在二叉搜索树中查找特定值
    public TreeNode searchBST(TreeNode root, int target) {
        // 如果根节点为空，直接返回null
        if (root == null) {
            return null;
        }
        
        // 如果根节点的值大于目标值，那么目标值一定在左子树上（因为二叉搜索树的性质是左子节点的值小于根节点的值），所以在左子树上递归查找，然后返回左子树的结果。
        if (root.val > target) {
            return searchBST(root.left, target);
        }
        // 如果根节点的值小于目标值，那么目标值一定在右子树上（因为二叉搜索树的性质是右子节点的值大于根节点的值），所以在右子树上递归查找
        if (root.val < target) {
            return searchBST(root.right, target);
        }
        // 如果根节点的值等于目标值，那么就找到了目标节点，直接返回根节点
        return root;
    }
}
  • 时间复杂度： O(N)O(N) ，其中 NN 是二叉搜索树的节点数。最坏情况下二叉搜索树是一条链，且要找的元素比涟末尾的元素值还要小（大），这种情况下我们需要递归 NN 次。
  • 空间复杂度： O(N)O(N) 。最坏情况下递旧需要 O(N)O(N) 的栈空间。

迭代+二分

从根节点前进，直到遇到target或走到null。

根据大小关系确定前进方向，向左还是向右。二叉搜索树因为有序，所以迭代方法效率很高，每次可以排除一个子树，且空间复杂度低。常用。

如果找到目标值，则提前返回，返回当前节点。否则会一直前进到null，然后返回null

迭代和递归的区别是：迭代是在循环中前进，递归是利用子递归前进。

class Solution {
    // 主函数，用于在二叉搜索树中查找特定值
    public TreeNode searchBST(TreeNode root, int val) {
        // 这是一个循环，直到找到目标值或者遍历完所有节点（即root为null）
        while (root != null) {
            // 如果找到目标值，则提前返回，返回当前节点
            if (val == root.val) {
                return root;
            }
            // 如果当前节点的值大于目标值，那么目标值一定在左子树上（因为二叉搜索树的性质是左子节点的值小于根节点的值）
            // 如果当前节点的值小于目标值，那么目标值一定在右子树上（因为二叉搜索树的性质是右子节点的值大于根节点的值）
            // 所以，根据目标值和当前节点的值的大小关系，选择去左子树还是右子树继续查找
            root = val < root.val ? root.left : root.right;
        }
        // 如果遍历完所有节点都没有找到目标值，返回null
        return null;
    }
}
  • 时间复杂度：O(n)O(n) ，其中 nn 是二叉搜索树的节点数。最坏情况下二叉搜索树是一条链，且要找的元素比涟末尾的元素值还要小（大），这种情况下我们需要递归 nn 次。
  • 空间复杂度：O(1)O(1)。