538. 把二叉搜索树转换为累加树

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

• 节点的左子树仅包含键 小于 节点键的节点。
• 节点的右子树仅包含键 大于 节点键的节点。
• 左右子树也必须是二叉搜索树。

注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

示例 1：

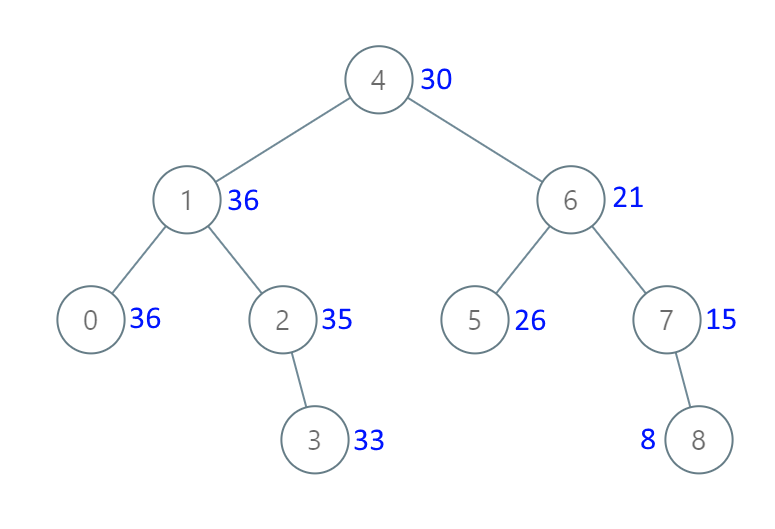
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

• 树中的节点数介于 0 和 104 之间。
• 每个节点的值介于 -104 和 104 之间。
• 树中的所有值 互不相同 。
• 给定的树为二叉搜索树。

回溯，反序中序遍历，无返回值。

class Solution {
    public TreeNode convertBST(TreeNode root) {
        traverse(root);
        return root;
    }

    // 记录累加和，全局变量
    int sum = 0;
    void traverse(TreeNode root) {
        if (root == null) {
            return;
        }
        
        traverse(root.right);
        // 维护累加和
        sum += root.val;
        // 将 BST 转化成累加树
        root.val = sum;
        traverse(root.left);
    }
}

• 时间复杂度O(n)，n是二叉树的节点总数。
• 空间复杂度O(h)，h是树的高度。

Morris 反序中序遍历

有一种巧妙的方法可以在线性时间内，只占用常数空间来实现中序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出，因此被称为 Morris 遍历。

Morris 遍历的核心思想是利用树的大量空闲指针，实现空间开销的极限缩减。其反序中序遍历规则总结如下：

• 如果当前节点的右子节点为空，处理当前节点，并遍历当前节点的左子节点；
• 如果当前节点的右子节点不为空，找到当前节点右子树的最左节点（该节点为当前节点中序遍历的前驱节点）；
  • 如果最左节点的左指针为空，将最左节点的左指针指向当前节点，遍历当前节点的右子节点；
  • 如果最左节点的左指针不为空（即已经遍历过该节点），将最左节点的左指针重新置为空（恢复树的原状），处理当前节点，并将当前节点置为其左节点；

重复步骤 1 和步骤 2，直到遍历结束。

这样我们利用 Morris 遍历的方法，反序中序遍历该二叉搜索树，即可实现线性时间与常数空间的遍历。

class Solution {
    public TreeNode convertBST(TreeNode root) {
        int sum = 0; // 累加和
        TreeNode node = root; // 当前遍历的节点

        // 使用 Morris 中序遍历的逆序遍历实现
        while (node != null) {
            if (node.right == null) {
                // 如果当前节点没有右子节点
                sum += node.val; // 更新累加和
                node.val = sum; // 更新当前节点的值
                
                node = node.left; // 移动到左子节点
            } else {
                // 如果当前节点有右子节点
                TreeNode succ = getSuccessor(node); // 找到当前节点的后继节点
                if (succ.left == null) {
                    // 如果后继节点的左子节点为空，将当前节点设为后继节点的左子节点
                    succ.left = node;
                    node = node.right; // 移动到右子节点
                } else {
                    // 如果后继节点的左子节点已经指向当前节点，将其恢复为空
                    succ.left = null;
                    
                    sum += node.val; // 更新累加和
                    node.val = sum; // 更新当前节点的值
                    
                    node = node.left; // 移动到左子节点
                }
            }
        }

        return root; // 返回累加树的根节点
    }

    public TreeNode getSuccessor(TreeNode node) {
        TreeNode succ = node.right; // 后继节点初始为当前节点的右子节点
        // 找到后继节点的最左子节点。重点：succ.left != node
        while (succ.left != null && succ.left != node) {
            succ = succ.left;
        }
        return succ; // 返回后继节点
    }
}

• 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。没有右子树的节点只被访问一次，有右子树的节点被访问两次。
• 空间复杂度：O(1)。只操作已经存在的指针（树的空闲指针），因此只需要常数的额外空间。