102. 二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

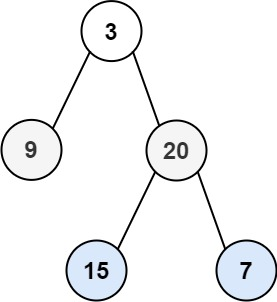
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 [0, 2000] 内
• -1000 <= Node.val <= 1000

BFS

入队第一层节点，逐个弹出第一层节点并获取子节点，并把子节点入队，也就是说，操作完后队列里存的是一整层的节点。 用这个队列这样做是为了弹出节点，我们会把弹出的每一层的节点存在一个链表中，这样所有的链表就是层序遍历的结果。 queue和level中都存当前层的节点，但是queue会弹出以存储下一层的节点，level是链表，不会弹出，且一层对应一个level。

它和普通广度优先搜索的区别在于，普通广度优先搜索每次只取一个元素拓展，而这里每次取 $s_i$ 个元素。 在上述过程中的第 $i$ 次迭代就得到了二叉树的第 $i$ 层的 $s_i$ 个元素。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        // 最终结果列表，存储每一层的节点值
        List<List<Integer>> ret = new ArrayList<List<Integer>>();
        // 如果根节点为空，则直接返回空结果
        if (root == null) {
            return ret;
        }
        // 使用队列来实现广度优先搜索
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        // 首先将根节点入队
        queue.offer(root);

        
        // 当队列不为空时，循环执行以下操作
        // 队列里存节点，level里存节点的值
        while (!queue.isEmpty()) {
            // 存储当前层的节点值
            List<Integer> level = new ArrayList<Integer>();
            // 遍历当前层的所有节点。重点。
            for (int i = 0; i < queue.size(); i++) {
                // 从队列中取出一个节点
                TreeNode node = queue.poll();
                // 将该节点的值加入到当前层的列表中。重点。
                level.add(node.val);
                
                // 如果该节点有左子节点，则将左子节点入队
                if (node.left != null) {
                    queue.offer(node.left);
                }
                // 如果该节点有右子节点，则将右子节点入队
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
            
            // 将当前层的节点值列表加入到最终结果列表中
            ret.add(level);
        }
        
        // 返回最终结果
        return ret;
    }
}

记树上所有节点的个数为 n。

• 时间复杂度：每个点进队出队各一次，故渐进时间复杂度为 O(n)。
• 空间复杂度：队列中元素的个数不超过 n 个，故渐进空间复杂度为 O(n)。

无返回值有信息参数的 DFS

利用变量记录dfs的层级，然后把该层级的节点放到链表的索引（等于该层级，如果层级越界，则新建链表）对应的链表中。

DFS的过程中记录下每个节点所在的层数，然后按层数添加节点。

先看根节点，再看叶子节点，再看结束条件。

class Solution {
    // 结果列表，存储每一层的节点值
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> levelOrder(TreeNode root) {
        // 从根节点开始深度优先搜索，0表示根节点的层级
        dfs(root, 0);
        return res;
    }
    
    // 递归函数，node为当前节点，idx为当前节点的层级。idx是重点。
    private void dfs(TreeNode node, int idx) {
        // 如果当前节点为空，则返回，不再进行后续操作
        if (node == null) return;
        
        // 如果当前层级还没有对应的列表（即第一次访问这个层级的节点）
        // 那么在结果列表中添加一个新的列表用于存储这一层的节点值
        // 注意 == res.size() 也是越界，因为 res 最远的索引是 res.size() - 1.
        if (idx >= res.size()) {
            res.add(new ArrayList<>());
        }
        // 将当前节点的值加入到它所在层级的列表中
        res.get(idx).add(node.val);
        
        // 递归地对当前节点的左子节点进行深度优先搜索
        // 左子节点的层级是当前节点层级+1
        // dfs 什么时候返回呢？遍历完当前节点的所有子节点就会返回。
        dfs(node.left, idx + 1);
        // 同理，递归地对当前节点的右子节点进行深度优先搜索
        dfs(node.right, idx + 1);
        // 注意，对左右子节点的递归调用完成后，当前层的递归函数实例才会返回
        // 这意味着当前节点的所有子节点已经被遍历完毕
    }
}

代码的时间复杂度主要由递归遍历二叉树的操作决定。代码中，每个节点都被访问了一次，并且在每个节点上进行了常数时间的操作（添加节点值到列表中）。

1. 遍历节点：
   • 递归函数 dfs 对每个节点访问一次，因此访问节点的总次数是 O(n)，其中 n 是二叉树中的节点数。
2. 操作分析：
   • 对于每个节点，首先检查是否为 null，然后检查并添加当前节点值到结果列表中，这些操作都是常数时间 O(1)。

空间复杂度包括以下几个方面：

1. 递归调用栈：
   • 递归深度最大为二叉树的高度 h。在最坏情况下，树是完全不平衡的，树的高度为 n，此时递归调用栈的空间复杂度为 O(n)。
   • 在最好情况下，树是完全平衡的，树的高度为 log(n)，此时递归调用栈的空间复杂度为 O(log(n))。
2. 结果列表 res：
   • 结果列表 res 存储了所有节点的值，空间复杂度为 O(n)，因为每个节点的值都需要存储在列表中。